题目内容
19.在?ABCD中,∠ABC的角平分线BE交AD所在直线于点E,AD=5,DE=1,则AB=4或6.分析 分两种情况:①如图1,在?ABCD中,根据平行线和角平分线的性质得到△ABE是等腰三角形,于是得到AB=AE,根据已知条件即可得到结果;
②如图2,方法同①.
解答 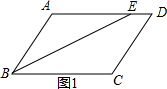 解:①如图1,在?ABCD中,
解:①如图1,在?ABCD中,
∵AD∥BC,
∴∠AEB=∠CBE,
∵BE平分∠ABC,
∴∠ABE=∠EBC,
∴∠ABE=∠AEB,
∴AB=AE,
∵AD=5,DE=1,
∴AB=AE=4;
②如图2,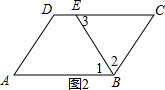 在?ABCD中,
在?ABCD中,
∵AB∥DC,BC=AD=5,AB=CD,
∴∠1=∠3,
∵BE平分∠ABC,
∴∠1=∠2,
∴∠2=∠3,
∴BC=CE,
∵BC=5,
∴CE=5,∵DE=1,
∴AB=CD=6,
综上所述:AB=4或6,
故答案为:4或6.
点评 本题主要考查对平行四边形的性质,平行线的性质,角平分线的性质,等腰三角形的判定等知识点的理解和掌握,能综合运用这些性质进行计算是解此题的关键.

练习册系列答案
相关题目
7.过平行四边形ABCD的顶点A、C分别作对角线BD的垂线,垂足是E、F,则四边形AECF是( )
| A. | 任意四边形 | B. | 平行四边形 | C. | 矩形 | D. | 菱形 |
9.数轴上点M到1的距离是5,则点M表示的数是( )
| A. | 6 | B. | -4 | C. | 6或-4 | D. | 不能确定 |