题目内容
15.如图①所示,已知A、B为直线l上两点,点C为直线l上方一动点,连接AC、BC,分别以AC、BC为边向△ABC外作正方形CADF和正方形CBEG,过点D作DD1⊥l于点D1,过点E作EE1⊥l于点E1.(1)如图②,当点E恰好在直线l上时(此时E1与E重合),请直接写出DD1与AB之间的数量关系:DD1=AB.
(2)在图①中,当D、E两点都在直线l的上方时,试探索三条线段DD1、EE1、AB之间的数量关系,并说明理由.
(3)如图③,当点E在直线l的下方时,请直接写出三条线段DD1、EE1、AB之间的数量关系:AB=DD1-EE1.
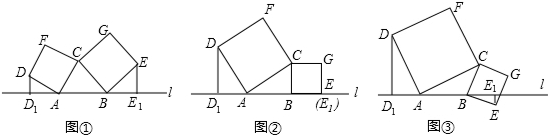
分析 (1)由四边形CADF、CBEG是正方形,可得AD=CA,∠DAC=∠ABC=90°,又由同角的余角相等,求得∠ADD1=∠CAB,然后利用AAS证得△ADD1≌△CAB,根据全等三角形的对应边相等,即可得DD1=AB;
(2)首先过点C作CH⊥AB于H,由DD1⊥AB,可得∠DD1A=∠CHA=90°,由四边形CADF是正方形,可得AD=CA,又由同角的余角相等,求得∠ADD1=∠CAH,然后利用AAS证得△ADD1≌△CAH,根据全等三角形的对应边相等,即可得DD1=AH,同理EE1=BH,则可得AB=DD1+EE1.
(3)证明方法同(2),易得AB=DD1-EE1.
解答 (1)证明:∵四边形CADF、CBEG是正方形,
∴AD=CA,∠DAC=∠CBE=90°,
∴∠DAD1+∠CAB=90°,
∵DD1⊥AB,
∴∠DD1A=∠ABC=90°,
∴∠DAD1+∠ADD1=90°,
∴∠ADD1=∠CAB,
在△ADD1和△CAB中,
$\left\{\begin{array}{l}{∠D{D}_{1}A=∠ABC}\\{∠AD{D}_{1}=∠CAB}\\{AD=CA}\end{array}\right.$,
∴△ADD1≌△CAB(AAS),
∴DD1=AB;
故答案为:DD1=AB;
(2)解:AB=DD1+EE1.
证明:如图①,过点C作CH⊥AB于H,
∵DD1⊥AB,
∴∠DD1A=∠CHA=90°,
∴∠DAD1+∠ADD1=90°,
∵四边形CADF是正方形,
∴AD=CA,∠DAC=90°,
∴∠DAD1+∠CAH=90°,
∴∠ADD1=∠CAH,
在△ADD1和△CAH中,
$\left\{\begin{array}{l}{∠D{D}_{1}A=∠CHA}\\{∠AD{D}_{1}=∠CAH}\\{AD=CA}\end{array}\right.$,
∴△ADD1≌△CAH(AAS),
∴DD1=AH;
同理:EE1=BH,
∴AB=AH+BH=DD1+EE1;
(3)解:AB=DD1-EE1.
证明:如图③,过点C作CH⊥AB于H,
∵DD1⊥AB,
∴∠DD1A=∠CHA=90°,
∴∠DAD1+∠ADD1=90°,
∵四边形CADF是正方形,
∴AD=CA,∠DAC=90°,
∴∠DAD1+∠CAH=90°,
∴∠ADD1=∠CAH,
在△ADD1和△CAH中,
$\left\{\begin{array}{l}{∠D{D}_{1}A=∠CHA}\\{∠AD{D}_{1}=∠CAH}\\{AD=CA}\end{array}\right.$,
∴△ADD1≌△CAH(AAS),
∴DD1=AH;
同理:EE1=BH,
∴AB=AH-BH=DD1-EE1,
故答案为:AB=DD1-EE1.
点评 本题考查了正方形的性质的运用,全等三角形的判定及性质的运用,直角三角形的性质的运用,解答时证明三角形全等是关键.

| A. | 扩大5倍 | B. | 扩大10倍 | C. | 不变 | D. | 缩小5倍 |
| A. | 任意四边形 | B. | 平行四边形 | C. | 矩形 | D. | 菱形 |
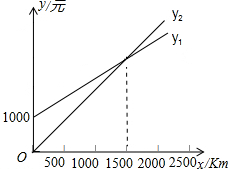 某单位计划与某个体车主或某国营出租车公司中的一家签订月租车合同,设汽车每月行驶x km,应付给个体车主的月租费为y1元,付给出租车公司的月租费为y2元,在同一直角坐标系中y1、y2与x的函数图象如图所示,观察图象回答下列问题:
某单位计划与某个体车主或某国营出租车公司中的一家签订月租车合同,设汽车每月行驶x km,应付给个体车主的月租费为y1元,付给出租车公司的月租费为y2元,在同一直角坐标系中y1、y2与x的函数图象如图所示,观察图象回答下列问题: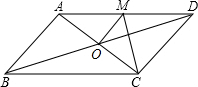 如图,?ABCD的对角线AC、BD相交于点O,过点O的直线OM⊥AC.已知△CDM的周长是22cm.则?ABCD的周长是44cm.
如图,?ABCD的对角线AC、BD相交于点O,过点O的直线OM⊥AC.已知△CDM的周长是22cm.则?ABCD的周长是44cm.