题目内容
1.计算题(1)($\sqrt{5}$+1)0-$\sqrt{12}$+|-$\sqrt{3}$|
(2)$(\sqrt{27}+\sqrt{20})+(\sqrt{75}-\sqrt{5})$
(3)$\frac{1}{2}\sqrt{8}-\sqrt{0.5}-\sqrt{4\frac{1}{2}}+2\sqrt{50}$
(4)$(3\sqrt{27}-2\sqrt{48})÷\sqrt{3}$
(5)$(\sqrt{2}+3)(\sqrt{2}-5)$
(6)$(\sqrt{3}+\sqrt{2})(\sqrt{3}-\sqrt{2})+{(\sqrt{2}+1)^2}$.
分析 (1)根据零指数幂的意义和绝对值的意义得到原式=1-2$\sqrt{3}$+$\sqrt{3}$,然后合并即可;
(2)先把各二次根式化为最简二次根式,然后去括号合并即可;
(3)先把各二次根式化为最简二次根式,然后合并即可;
(4)先把各二次根式化为最简二次根式,然后把括号内合并后进行二次根式的除法运算;
(5)利用多项乘法展开,然后合并即可;
(6)利用平方差公式和完全平方公式计算.
解答 解:(1)原式=1-2$\sqrt{3}$+$\sqrt{3}$=1-$\sqrt{3}$;
(2)原式=3$\sqrt{3}$+2$\sqrt{5}$+5$\sqrt{3}$-$\sqrt{5}$=8$\sqrt{3}$+$\sqrt{5}$;
(3)原式=$\sqrt{2}$-$\frac{\sqrt{2}}{2}$-$\frac{3\sqrt{2}}{2}$+10$\sqrt{2}$=9$\sqrt{2}$;
(4)原式=(9$\sqrt{3}$-8$\sqrt{3}$)$÷\sqrt{3}$=$\sqrt{3}$÷$\sqrt{3}$=1;
(5)原式=2-5$\sqrt{2}$+3$\sqrt{2}$-15=-2$\sqrt{2}$-13;
(6)原式=3-2+2+2$\sqrt{2}$+1=4+2$\sqrt{2}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.以下列长度为三边的三角形,哪个不能组成直角三角形( )
| A. | 3,4,5 | B. | 5,12,13 | C. | 6,8,10 | D. | 2,3,4 |
6.下列性质中,平行四边形不一定具备的是( )
| A. | 对边平行 | B. | 对角互补 | C. | 对角线互相平分 | D. | 对边相等 |
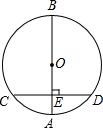 如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=10,CD=8,那么线段AE的长为( )
如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=10,CD=8,那么线段AE的长为( )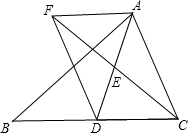 已知:如图,在△ABC中,D是BC边上的一点,连接AD,取AD的中点E,过点A作BC的平行线与CE的延长线交于点F,连接DF.
已知:如图,在△ABC中,D是BC边上的一点,连接AD,取AD的中点E,过点A作BC的平行线与CE的延长线交于点F,连接DF.