题目内容
14.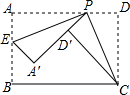 如图,有一张矩形纸片ABCD,AB=3,BC=4,点P是AD边上任意一点(与点A,D不重合),现将△PCD沿PC翻折,得到△PCD′,再在AB边上选取适当的点E,将△PAE沿PE翻折,得到△PA′E,并使直线PD′,PA重合,线段AE的最大值为$\frac{4}{3}$.
如图,有一张矩形纸片ABCD,AB=3,BC=4,点P是AD边上任意一点(与点A,D不重合),现将△PCD沿PC翻折,得到△PCD′,再在AB边上选取适当的点E,将△PAE沿PE翻折,得到△PA′E,并使直线PD′,PA重合,线段AE的最大值为$\frac{4}{3}$.
分析 可设AE=x,PD=y,根据翻折的性质可得到∠EPC=90°,从而可以推证△EA'P∽△PD'C,通过相似三角形对应边的比找到y与x的关系式,利用配方法得到x的最大值.
解答 解:∵由题意可知∠APE=∠EPA′,∠DPC=∠D′PC,AP=A′P,DC=D′C
∴∠EPC=90°,
∵∠A=∠A′=90°,∠D=∠PD′C=90°,
∴∠A′EP=∠D′PC,
∴△EA'P∽△PD'C
∴$\frac{EA′}{PD′}=\frac{A′P}{D′C}$
设AE=x,PD=y,
∵AB=3,BC=4,
∴AP=4-y,
∴$\frac{x}{y}=\frac{4-y}{4}$,整理得x=-$\frac{1}{3}$(y-2)2+$\frac{4}{3}$,
∴x的最大值为$\frac{4}{3}$.
故答案为$\frac{4}{3}$.
点评 本题考查了折叠的性质及相似三角形性质,解题的关键是利用折叠的性质找到相似三角形,从而找到两条折叠线段之间的关系确定最大值.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
2.下列计算,正确的是( )
| A. | -|-3|=-3 | B. | 30=0 | C. | 3-1=-$\frac{1}{3}$ | D. | $\root{3}{9}$=3 |
9.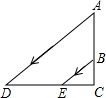 如图,阳光从教室的窗户射入室内,窗户框AB在地面上的影长DE=1.8m,窗户下檐到地面的距离BC=1m,EC=1.2m,那么窗户的高AB为( )
如图,阳光从教室的窗户射入室内,窗户框AB在地面上的影长DE=1.8m,窗户下檐到地面的距离BC=1m,EC=1.2m,那么窗户的高AB为( )
 如图,阳光从教室的窗户射入室内,窗户框AB在地面上的影长DE=1.8m,窗户下檐到地面的距离BC=1m,EC=1.2m,那么窗户的高AB为( )
如图,阳光从教室的窗户射入室内,窗户框AB在地面上的影长DE=1.8m,窗户下檐到地面的距离BC=1m,EC=1.2m,那么窗户的高AB为( )| A. | 1.5m | B. | 1.6m | C. | 1.86m | D. | 2.16m |
19.下列一元二次方程有两个相等实数根的是( )
| A. | x2+3=0 | B. | (x+1)2=0 | C. | x2+2x=0 | D. | (x+3)(x-1)=0 |
19.下列方程中,不是一元二次方程的是( )
| A. | x2=-3 | B. | -4x2+2x+1=0 | C. | 3x2-2x+1=0 | D. | x2+x=(x+1)(x-2) |
 如图,在矩形ABCD中,对角线AC、BD相交于点O,过点O作EF⊥AC分别交AD、BC于F、E.
如图,在矩形ABCD中,对角线AC、BD相交于点O,过点O作EF⊥AC分别交AD、BC于F、E.