题目内容
1. 甲、乙两车从A地出发沿同一路线驶向B地,甲车先出发匀速驶向B地.40分钟后,乙车出发,匀速行驶一段时间后,在途中的货站装货耗时半小时,由于满载货物,为了行驶安全,速度减少了50千米/时,结果与甲车同时到达B地,甲乙两车距A地的路程y(千米)与乙车行驶时间x(时)之间的函数图象如图所示,下列说法:
甲、乙两车从A地出发沿同一路线驶向B地,甲车先出发匀速驶向B地.40分钟后,乙车出发,匀速行驶一段时间后,在途中的货站装货耗时半小时,由于满载货物,为了行驶安全,速度减少了50千米/时,结果与甲车同时到达B地,甲乙两车距A地的路程y(千米)与乙车行驶时间x(时)之间的函数图象如图所示,下列说法:①a=4.5;
②甲的速度是60千米/时;
③乙出发80分钟追上甲;
④乙刚到达货站时,甲距B地180千米;
其中正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 由线段DE所代表的意思,结合装货半小时,可得出a的值,从而判断出①成立;
结合路程=速度×时间,能得出甲车的速度,从而判断出②成立;
设出乙车刚出发时的速度为x千米/时,则装满货后的速度为(x-50)千米/时,由路程=速度×时间列出关于x的一元一次方程,解出方程即可得知乙车的初始速度,由甲车先跑的路程÷两车速度差即可得出乙车追上甲车的时间,从而得出③成立;
由乙车刚到达货站的时间,可以得出甲车行驶的总路程,结合A、B两地的距离即可判断④也成立.
综上可知①②③④皆成立.
解答 解:∵线段DE代表乙车在途中的货站装货耗时半小时,
∴a=4+0.5=4.5(小时),即①成立;
40分钟=$\frac{2}{3}$小时,
甲车的速度为460÷(7+$\frac{2}{3}$)=60(千米/时),
即②成立;
设乙车刚出发时的速度为x千米/时,则装满货后的速度为(x-50)千米/时,
根据题意可知:4x+(7-4.5)(x-50)=460,
解得:x=90.
乙车发车时,甲车行驶的路程为60×$\frac{2}{3}$=40(千米),
乙车追上甲车的时间为40÷(90-60)=$\frac{4}{3}$(小时),
$\frac{4}{3}$小时=80分钟,即③成立;
乙车刚到达货站时,甲车行驶的时间为(4+$\frac{2}{3}$)小时,
此时甲车离B地的距离为460-60×(4+$\frac{2}{3}$)=180(千米),
即④成立.
综上可知正确的有:①②③④.
故选D.
点评 本题考查了一次函数的应用,解题的关键是知道各数量间的关系结合图形找出结论.本题属于中档题型,难度不大,但是判定的过程稍显繁琐,解决该类题型的方法是掌握各数量间的关系结合行程得出结论.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
11.下列各式,能用平方差公式计算的是( )
| A. | (a-1)(a+1) | B. | (a-3)(-a+3) | C. | (a+2b)(2a-b) | D. | (-a-3)2 |
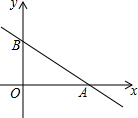 已知:如图,直线y=-$\frac{1}{2}$x+1与x轴、y轴的交点分别是A和B,把线段AB绕点A顺时针旋转90°得线段AB′.
已知:如图,直线y=-$\frac{1}{2}$x+1与x轴、y轴的交点分别是A和B,把线段AB绕点A顺时针旋转90°得线段AB′.