题目内容
10.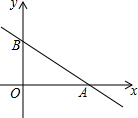 已知:如图,直线y=-$\frac{1}{2}$x+1与x轴、y轴的交点分别是A和B,把线段AB绕点A顺时针旋转90°得线段AB′.
已知:如图,直线y=-$\frac{1}{2}$x+1与x轴、y轴的交点分别是A和B,把线段AB绕点A顺时针旋转90°得线段AB′.(1)直接写出点B′的坐标;
(2)若点C(1,a)在第一象限内,并且S△ABC=S△ABB′,求a的值;
(3)P在x轴上,且△PAB是等腰三角形,请直接写出点P的坐标.
分析 (1)根据已知条件得到△AOB≌△AEB′,根据全等三角形的性质得到AE=OB,B′E=OA=2,即可得到结论;
(2)根据勾股定理得到AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{5}$,根据三角形的面积公式得到S△ABB′=$\frac{1}{2}$AB2=$\frac{5}{2}$,于是得到S△ABC=$\frac{1}{2}$CM×2=|a-0.5|=$\frac{5}{2}$.即可得到结论;
(3)分三种情况,①当AB=AP=$\sqrt{5}$时,②当AB=BP=$\sqrt{5}$,③当PA=PB,即点P在AB的垂直平分线上,根据相似三角形的性质即可得到结论.
解答 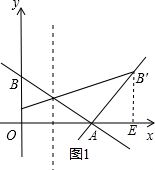 解:(1)如图1:过B′作B′E⊥x轴于E,
解:(1)如图1:过B′作B′E⊥x轴于E,
∵直线y=-$\frac{1}{2}$x+1与x轴、y轴的交点分别是A和B,
∴A(2,0),B(0,1),过B′作B′E⊥x轴于E,
∵∠AOB=∠B′EA=∠BAB′=90°,
∴∠ABO+∠BAO=∠BAO+∠AB′E=90°,
∴∠BAO=∠AB′E,
在△AOB与△AB′E中,$\left\{\begin{array}{l}{∠AOB=∠AEB′}\\{∠BAO=∠AB′E}\\{AB=AB′}\end{array}\right.$,
∴△AOB≌△AEB′,
∴AE=OB,B′E=OA=2,
∴OE=3,
∴点B′(3,2);
(2)∵△ABB′为等腰直角三角形,
直角边AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{5}$,
∴S△ABB′=$\frac{1}{2}$AB2=$\frac{5}{2}$,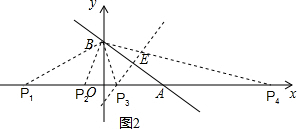
在y=-$\frac{1}{2}$x+1中,当x=1时,y=0.5.
即直线x=1与AB交于点M(1,0.5).
又∵点A和B到CM的距离之和显然为2,
∴S△ABC=$\frac{1}{2}$CM×2=|a-0.5|=$\frac{5}{2}$.
解得a=3;
(3)①当AB=AP=$\sqrt{5}$时,
∴OP=OA+AP=2+$\sqrt{5}$,或OP=AP-OA=$\sqrt{5}$-2,
∴P2(2-$\sqrt{5}$,0).P4(2+$\sqrt{5}$,0),
②当AB=BP=$\sqrt{5}$,
∴OP=OA=2,
∴P1(-2,0),
③当PA=PB,即点P在AB的垂直平分线上,
∴AE=$\frac{1}{2}$AB=$\frac{\sqrt{5}}{2}$,
∴△APE∽△ABO,
∴$\frac{AE}{OA}=\frac{AP}{AB}$,即$\frac{\frac{\sqrt{5}}{2}}{2}=\frac{AP}{\sqrt{5}}$,
∴AP=$\frac{5}{4}$,
∴OP=2-$\frac{5}{4}$=$\frac{3}{4}$,
∴P3($\frac{3}{4}$,0),
∴P点的坐标为:(-2,0),(2-$\sqrt{5}$,0),(2+$\sqrt{5}$,0),($\frac{3}{4}$,0).
点评 本题考查了一次函数的综合,全等三角形的判定和性质,相似三角形的判定和性质,勾股定理,等腰三角形的性质,正确的作出图形是解题的关键.

| A. | 1 | B. | 0 | C. | $\frac{3}{2}$ | D. | -2 |
| A. | -5 | B. | $-\sqrt{2}$ | C. | 1 | D. | π |
 甲、乙两车从A地出发沿同一路线驶向B地,甲车先出发匀速驶向B地.40分钟后,乙车出发,匀速行驶一段时间后,在途中的货站装货耗时半小时,由于满载货物,为了行驶安全,速度减少了50千米/时,结果与甲车同时到达B地,甲乙两车距A地的路程y(千米)与乙车行驶时间x(时)之间的函数图象如图所示,下列说法:
甲、乙两车从A地出发沿同一路线驶向B地,甲车先出发匀速驶向B地.40分钟后,乙车出发,匀速行驶一段时间后,在途中的货站装货耗时半小时,由于满载货物,为了行驶安全,速度减少了50千米/时,结果与甲车同时到达B地,甲乙两车距A地的路程y(千米)与乙车行驶时间x(时)之间的函数图象如图所示,下列说法: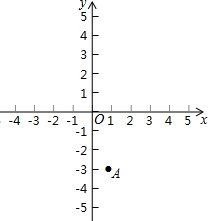 已知反比例函数y1=$\frac{k}{x}$与一次函数y2=mx+n的图象都经过A(1,-3),且当x=-3时,两个函数的函数值相等
已知反比例函数y1=$\frac{k}{x}$与一次函数y2=mx+n的图象都经过A(1,-3),且当x=-3时,两个函数的函数值相等