题目内容
8.已知,点M、N分别是正方形ABCD的边CB、CD的延长线上的点,连接AM、AN、MN,∠MAN=135°.(友情提醒:正方形的四条边都相等,即AB=BC=CD=DA;四个内角都是90°,即∠ABC=∠BCD=∠CDA=∠DAB=90°)(1)如图①,若BM=DN,求证:MN=BM+DN.
(2)如图②,若BM≠DN,试判断(1)中的结论是否仍成立?若成立,请给予证明;若不成立,请说明理由.

分析 (1)作AE⊥MN,垂足为E.证明△ADN≌△ABM.得到AN=AM,∠NAD=∠MAB.再证明△ADN≌△AEN.得到DN=EN,即可解答.
(2)利用已知条件证明△ABP≌△ADN,得到AP=AN,∠BAP=∠DAN.再证明∠MAN=∠MAP.从而证明△ANM≌△APM,得到MN=MP,由MP=BM+BP=BM+DN,即可得到MN=BM+DN.
解答 解:(1)如图①,作AE⊥MN,垂足为E.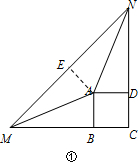
∵四边形ABCD是正方形,
∴AD=AB,∠ADC=∠ABC=90°,
∴∠ADN=∠ABM=90°.
在△ADN与△ABM中,
$\left\{\begin{array}{l}{AD=AB}\\{∠ADN=∠ABM=90°}\\{DN=BM}\end{array}\right.$,
∴△ADN≌△ABM.
∴AN=AM,∠NAD=∠MAB.
∵∠MAN=135°,∠BAD=90°,
∴∠NAD=∠MAB=$\frac{1}{2}$(360°-135°-90°)=67.5°.
∴∠AND=∠AMB=22.5°,
∵AN=AM,∠MAN=135°,AE⊥MN,
∴MN=2NE,∠AMN=∠ANM=22.5°.
在△ADN与△AEN中,
∵$\left\{\begin{array}{l}{∠ADN=∠AEN=90°}\\{∠AND=∠ANM=22.5°}\\{AN=AN}\end{array}\right.$,
∴△ADN≌△AEN.
∴DN=EN.
∴MN=2EN=2DN=BM+DN.
(2)如图②,若BM≠DN,①中的结论仍成立,理由如下:
延长BC到点P,使BP=DN,连结AP.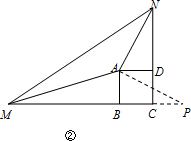
∵四边形ABCD是正方形,
∴AB=AD,∠ABC=∠ADC=∠BAD=90°.
∴∠ADN=90°.
在△ABP与△ADN中,
∵$\left\{\begin{array}{l}{AB=AD}\\{∠ABP=∠ADN}\\{BP=DN}\end{array}\right.$,
∴△ABP≌△ADN.
∴AP=AN,∠BAP=∠DAN.
∵∠MAN=135°,
∴∠MAP=∠MAB+∠BAP=∠MAB+∠DAN=360°-∠MAN-∠BAD=360°-135°-90°=135°.
∴∠MAN=∠MAP.
在△ANM与△APM中,
∵$\left\{\begin{array}{l}{AN=AP}\\{∠MAN=∠MAP}\\{AM=AM}\end{array}\right.$,
∴△ANM≌△APM.
∴MN=MP.
∵MP=BM+BP=BM+DN,
∴MN=BM+DN.
点评 本题考查了全等三角形的性质定理与判定定理,解决本题的关键是证明三角形全等.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案| A. | -4 | B. | 2 | C. | -1 | D. | 3 |
 如图,一次函数y=$\frac{3}{4}$x+3的图象与x轴交于A点,与y轴交于B,与正比例函数y=-$\frac{9}{4}$x的图象交于点C,则△AOC的面积为( )
如图,一次函数y=$\frac{3}{4}$x+3的图象与x轴交于A点,与y轴交于B,与正比例函数y=-$\frac{9}{4}$x的图象交于点C,则△AOC的面积为( )| A. | $\frac{9}{4}$ | B. | $\frac{9}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{3}{2}$ |
 如图,?ABCD中,E是BC边上一点,BE:EC=1:2,AE交BD于点F,则BF:FD等于( )
如图,?ABCD中,E是BC边上一点,BE:EC=1:2,AE交BD于点F,则BF:FD等于( )| A. | 5:7 | B. | 3:5 | C. | 1:3 | D. | 2:5 |
 如图,D、E、F分别是△ABC各边的中点,
如图,D、E、F分别是△ABC各边的中点, 如图,点O为弧AB所在圆的圆心,OA⊥OB,点P在弧AB上,AP的延长线与OB的延长线交于点C,过点C作CD⊥OP于D.若OP=3,PD=1,则OC=3$\sqrt{2}$.
如图,点O为弧AB所在圆的圆心,OA⊥OB,点P在弧AB上,AP的延长线与OB的延长线交于点C,过点C作CD⊥OP于D.若OP=3,PD=1,则OC=3$\sqrt{2}$.