题目内容
19. 完成以下推理,并在括号中写出相应的根据
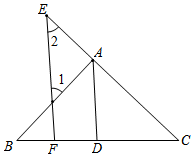
完成以下推理,并在括号中写出相应的根据如图,已知:AD⊥BC于点D,EF⊥BC于点F,且∠1=∠2,问AD平分∠BAC吗?说明理由.
解:AD平分∠BAC,理由如下:
∵AD⊥BC,EF⊥BC(已知),∴∠EFD=∠ADC=90°
∴EF∥AD(同位角相等,两直线平行)∴∠2=∠CAD,∠1=∠BAD
又∵∠1=∠2(已知),∴∠CAD=∠BAD∴AD平分∠BAC.
分析 根据题意易得AD∥FE且∠1=∠BAD,∠2=∠DAC,再根据等式的性质可得∠BAD=∠DAC,即可得出AD平分∠BAC.
解答  解:AD平分∠BAC,
解:AD平分∠BAC,
理由如下:
∵AD⊥BC,EF⊥BC(已知),
∴∠EFD=∠ADC=90°
∴EF∥AD,(同位角相等,两直线平行)
∴∠2=∠CAD,∠1=∠BAD,
又∵∠1=∠2(已知),
∴∠CAD=∠BAD,
∴AD平分∠BAC.
故答案为:(同位角相等,两直线平行),∠CAD,∠CAD=∠BAD.
点评 本题考查了平行线的判定和性质,以及角平分线的判定,解决问题的关键是运用角与角相互间的等量关系.

练习册系列答案
相关题目
9.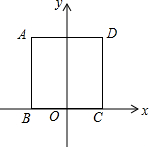 正方形ABCD在直角坐标系中如图放置,B点的坐标是(-2,0),C点的坐标是(2,0),则A点的坐标是( )
正方形ABCD在直角坐标系中如图放置,B点的坐标是(-2,0),C点的坐标是(2,0),则A点的坐标是( )
 正方形ABCD在直角坐标系中如图放置,B点的坐标是(-2,0),C点的坐标是(2,0),则A点的坐标是( )
正方形ABCD在直角坐标系中如图放置,B点的坐标是(-2,0),C点的坐标是(2,0),则A点的坐标是( )| A. | (4,-2) | B. | (-2,1) | C. | (2,4) | D. | (-2,4) |
10.下列各式变形正确的是( )
| A. | $\frac{2}{2+a}=\frac{1}{1+a}$ | B. | $\frac{1}{x+1}=\frac{x-1}{{{x^2}-1}}$ | C. | $\frac{-x+y}{x-y}=\frac{x+y}{y-x}$ | D. | $\frac{{{a^2}-1}}{a+1}=a-1$ |
9. 某地需要开辟一条隧道,隧道AB的长度无法直接测量.如图所示,在地面上取一点C,使C到A、B两点均可直接到达,测量找到AC和BC的中点D、E,测得DE的长为1100m,则隧道AB的长度为( )
某地需要开辟一条隧道,隧道AB的长度无法直接测量.如图所示,在地面上取一点C,使C到A、B两点均可直接到达,测量找到AC和BC的中点D、E,测得DE的长为1100m,则隧道AB的长度为( )
 某地需要开辟一条隧道,隧道AB的长度无法直接测量.如图所示,在地面上取一点C,使C到A、B两点均可直接到达,测量找到AC和BC的中点D、E,测得DE的长为1100m,则隧道AB的长度为( )
某地需要开辟一条隧道,隧道AB的长度无法直接测量.如图所示,在地面上取一点C,使C到A、B两点均可直接到达,测量找到AC和BC的中点D、E,测得DE的长为1100m,则隧道AB的长度为( )| A. | 3300 m | B. | 2200 m | C. | 1100 m | D. | 550 m |
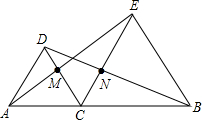 如图,△DAC和△EBC均是等边三角形,A、C、B三点在一条直线上,AE、BD分别与CD、CE交于点M、N.
如图,△DAC和△EBC均是等边三角形,A、C、B三点在一条直线上,AE、BD分别与CD、CE交于点M、N. 已知有理数a、b 在数轴上的位置如图所示.
已知有理数a、b 在数轴上的位置如图所示.