题目内容
12. 如图矩形ABCD中,AB=2,AD=4,矩形ABCD绕点A顺时针旋转90度,得到矩形AB′C′D′,则CC′=2$\sqrt{10}$.
如图矩形ABCD中,AB=2,AD=4,矩形ABCD绕点A顺时针旋转90度,得到矩形AB′C′D′,则CC′=2$\sqrt{10}$.
分析 矩形ABCD绕点A顺时针旋转90°得到矩形AB′C′D′,可知旋转中心为点A,旋转角∠CAC′=90°,根据对应点C、C′到旋转中心的距离相等可知,AC=AC′,先在Rt△ACD中用勾股定理求AC,再在Rt△CAC′中,利用勾股定理求CC′.
解答 解:由旋转的性质可知,∠CAC′=90°,AC=AC′,
Rt△ACD中,由勾股定理得,
AC=$\sqrt{A{D}^{2}+C{D}^{2}}$=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$,
在Rt△CAC′中,由勾股定理得,
CC′=$\sqrt{A{C}^{2}+AC{′}^{2}}$=2$\sqrt{10}$.
故答案为2$\sqrt{10}$.
点评 本题考查了旋转的性质,勾股定理的运用,属于基础题,需要熟练掌握.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
2.下列各式中计算正确的是( )
| A. | x5+x4=x9 | B. | x2•x3=x5 | C. | x3+x3=x6 | D. | (-x2)3=-x5 |
1.一个五次多项式与一个三次多项式的相加,所得结果的次数是( )
| A. | 八次 | B. | 五次 | C. | 三次 | D. | 不大于五次 |
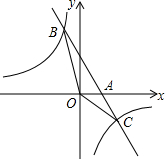 如图,已知一次函数y1=kx+b的图象与x轴相交于点A,与反比例函数y2=$\frac{c}{x}$相交于B(-1,5),C($\frac{5}{2}$,d)两点.
如图,已知一次函数y1=kx+b的图象与x轴相交于点A,与反比例函数y2=$\frac{c}{x}$相交于B(-1,5),C($\frac{5}{2}$,d)两点.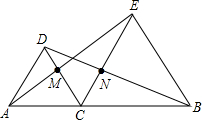 如图,△DAC和△EBC均是等边三角形,A、C、B三点在一条直线上,AE、BD分别与CD、CE交于点M、N.
如图,△DAC和△EBC均是等边三角形,A、C、B三点在一条直线上,AE、BD分别与CD、CE交于点M、N.