题目内容
10.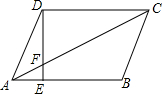 如图,平行四边形ABCD中,点E在AB边上,AE:EB=1:2,连结DE、AC交于点F,CF:CA=3:4;平行四边形被分成的4部分的面积比为1:3:9:11(从小到大).
如图,平行四边形ABCD中,点E在AB边上,AE:EB=1:2,连结DE、AC交于点F,CF:CA=3:4;平行四边形被分成的4部分的面积比为1:3:9:11(从小到大).
分析 根据平行四边形的性质得到AB=CD,AB∥CD,推出△AEF∽△CDF,根据相似三角形的性质得到$\frac{AF}{CF}=\frac{EF}{DF}=\frac{AE}{CD}=\frac{1}{3}$,于是得到CF:CA=3:4,S△ADF=3S△AEF,S△CDF=3S△ADF=9△AEF,即可得到结论.
解答 解:在平行四边形ABCD中,
∵AB=CD,AB∥CD,
∵AE:EB=1:2,
∴AE:AB=1:3,
∴AE:CD=1:3,
∵AB∥CD,
∴△AEF∽△CDF,
∴$\frac{AF}{CF}=\frac{EF}{DF}=\frac{AE}{CD}=\frac{1}{3}$,
∴CF:CA=3:4,
∴S△ADF=3S△AEF,S△CDF=3S△ADF=9△AEF,
∴S△ABC=S△ACD=12S△AEF,
∴S四边形BEFC=11S△AEF,
∴S△AEF:S△ADF:S△CDF:S四边形BEFC=1:3:9:11.
故答案为:3:4,1:3:9:11.
点评 本题考查了平行四边形的性质,相似三角形的判定和性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
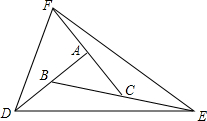 如图,△ABC的面积是10,将AB、BC、CA分别延长一倍到D、E、F,两两连接D、E、F,得到一个新的△DEF.则△DEF的面积为( )
如图,△ABC的面积是10,将AB、BC、CA分别延长一倍到D、E、F,两两连接D、E、F,得到一个新的△DEF.则△DEF的面积为( ) 如图,△ABC中,AD是角平分线.AE是高,∠B=60°,∠EAD=10°,求∠C.
如图,△ABC中,AD是角平分线.AE是高,∠B=60°,∠EAD=10°,求∠C.
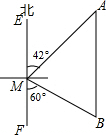 如图,一艘渔船位于小岛M的北偏东42°方向、距离小岛180海里的A处,渔船从A处沿正南方向航行一段距离后,到达位于小岛南偏东60°方向的B处.
如图,一艘渔船位于小岛M的北偏东42°方向、距离小岛180海里的A处,渔船从A处沿正南方向航行一段距离后,到达位于小岛南偏东60°方向的B处.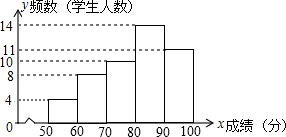 某班进行一次数学测试,根据测试成绩(得分为整数,满分为100分)绘制了频数分布图(如图所示,每组含最高分不含最低分),其中得分不超过50分的有3人,该班有5名学生的成绩为80分.根据所给信息解答下列问题:
某班进行一次数学测试,根据测试成绩(得分为整数,满分为100分)绘制了频数分布图(如图所示,每组含最高分不含最低分),其中得分不超过50分的有3人,该班有5名学生的成绩为80分.根据所给信息解答下列问题: