题目内容
等腰三角形一腰上的中线把这个三角形的周长分成12cm和21cm两部分,求这个等腰三角形的底边长.
考点:等腰三角形的性质,三角形三边关系
专题:
分析:作出图形,设AD=DC=x,BC=y,然后分两种情况列出方程组求解,再根据三角形的三边关系判断即可得解.
解答: 解:如图所示,设AD=DC=x,BC=y,由题意得
解:如图所示,设AD=DC=x,BC=y,由题意得
,或
,
解得
或
,
当
,等腰三角形的三边为8,8,17,显然不符合三角形的三边关系;
当
时,等腰三角形的三边为14,14,5,
所以,这个等腰三角形的底边长是5,
综上所述,这个等腰三角形的底边长5.
 解:如图所示,设AD=DC=x,BC=y,由题意得
解:如图所示,设AD=DC=x,BC=y,由题意得
|
|
解得
|
|
当
|
当
|
所以,这个等腰三角形的底边长是5,
综上所述,这个等腰三角形的底边长5.
点评:本题考查了等腰三角形的性质性质,三角形的三边关系,难点在于分情况讨论,作出图形更形象直观.

练习册系列答案
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
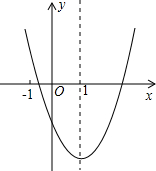 已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论错误的是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论错误的是( )| A、abc>0 |
| B、2a+b=0 |
| C、a-b+c>0 |
| D、4a+2b+c>0 |
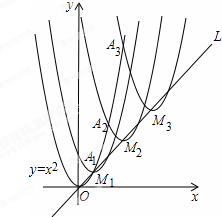 如图,抛物线y=x2在第一象限内经过的整数点(横坐标、纵坐标都为整数的点)依次为A1,A2,A3…An,….将抛物线y=x2沿直线L:y=x向上平移,得一系列抛物线,且满足下列条件:
如图,抛物线y=x2在第一象限内经过的整数点(横坐标、纵坐标都为整数的点)依次为A1,A2,A3…An,….将抛物线y=x2沿直线L:y=x向上平移,得一系列抛物线,且满足下列条件:①抛物线的顶点M1,M2,M3,…Mn,…都在直线L:y=x上;
②抛物线依次经过点A1,A2,A3…An,….
则顶点M2014的坐标为( )
| A、(2013,2013) |
| B、(2014,2014) |
| C、(4027,4027) |
| D、(4028,4028) |
二次函数y=x2的图象向左平移2个单位,得到新的图象的二次函数表达式是( )
| A、y=x2+2 |
| B、y=(x+2)2 |
| C、y=(x-2)2 |
| D、y=x2-2 |
 二次函数y=ax2+bx+c的图象如图所示.当y>0时,自变量x的取值范围是( )
二次函数y=ax2+bx+c的图象如图所示.当y>0时,自变量x的取值范围是( )| A、-3<x<1 |
| B、x<-1 |
| C、x>3 |
| D、x<-3或x>1 |
 抛物线
抛物线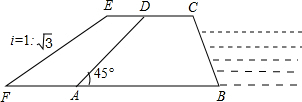 如图,某防洪指挥部发现长江边一处长100米,高8米,背水坡的坡角为45°的防洪大堤(横断面为梯形ABCD)急需加固.经调查论证,防洪指挥部专家组制定的加固方案是:沿背水坡面用土石进行加固,并使上底加宽3米,加固后背水坡EF的坡比i=1:
如图,某防洪指挥部发现长江边一处长100米,高8米,背水坡的坡角为45°的防洪大堤(横断面为梯形ABCD)急需加固.经调查论证,防洪指挥部专家组制定的加固方案是:沿背水坡面用土石进行加固,并使上底加宽3米,加固后背水坡EF的坡比i=1: 如图,AB为半圆的直径,且AB=3,半圆绕点B顺时针旋转45°,点A旋转到A′的位置,则图中阴影部分的面积为
如图,AB为半圆的直径,且AB=3,半圆绕点B顺时针旋转45°,点A旋转到A′的位置,则图中阴影部分的面积为