题目内容
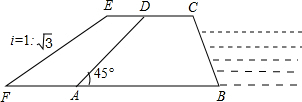 如图,某防洪指挥部发现长江边一处长100米,高8米,背水坡的坡角为45°的防洪大堤(横断面为梯形ABCD)急需加固.经调查论证,防洪指挥部专家组制定的加固方案是:沿背水坡面用土石进行加固,并使上底加宽3米,加固后背水坡EF的坡比i=1:
如图,某防洪指挥部发现长江边一处长100米,高8米,背水坡的坡角为45°的防洪大堤(横断面为梯形ABCD)急需加固.经调查论证,防洪指挥部专家组制定的加固方案是:沿背水坡面用土石进行加固,并使上底加宽3米,加固后背水坡EF的坡比i=1:| 3 |
(1)求加固后坝底增加的宽度AF;
(2)求完成这项工程需要土石多少立方米?(结果保留根号)
考点:解直角三角形的应用-坡度坡角问题
专题:
分析:(1)分别过E、D作AB的垂线,设垂足为G、H.在Rt△EFG中,根据坡面的铅直高度(即坝高)及坡比,即可求出水平宽FG的长;同理可在Rt△ADH中求出AH的长;由AF=FG+GH-AH求出AF的长.
(2)已知梯形AFED的上下底和高,易求得其面积,梯形AFED的面积乘以坝长即为所需的土石的体积.
(2)已知梯形AFED的上下底和高,易求得其面积,梯形AFED的面积乘以坝长即为所需的土石的体积.
解答:解:(1)分别过点E、D作EG⊥AB、DH⊥AB交AB于G、H.
∵四边形ABCD是梯形,且AB∥CD,
∴DH平行等于EG.
故四边形EGHD是矩形.
∴ED=GH.
在Rt△ADH中,
AH=DH=8(米).
在Rt△FGE中,
i=
=
,
∴FG=
EG=8
(米).
∴AF=FG+GH-AH=8
+3-8=8
-5(米);
(2)∵S梯形ADEF=
=(32
-8)(米2),
∴加宽部分的体积V=S梯形ADEF×坝长=(32
-8)×100=(3200
-800)(米3).
答:完成这项工程需要土石(3200
-800)米3.
∵四边形ABCD是梯形,且AB∥CD,

∴DH平行等于EG.
故四边形EGHD是矩形.
∴ED=GH.
在Rt△ADH中,
AH=DH=8(米).
在Rt△FGE中,
i=
| 1 | ||
|
| EG |
| FG |
∴FG=
| 3 |
| 3 |
∴AF=FG+GH-AH=8
| 3 |
| 3 |
(2)∵S梯形ADEF=
(3+8
| ||
| 2 |
| 3 |
∴加宽部分的体积V=S梯形ADEF×坝长=(32
| 3 |
| 3 |
答:完成这项工程需要土石(3200
| 3 |
点评:本题考查了解直角三角形的应用,解答本题的关键是理解坡度、坡比的含义,构造直角三角形,利用三角函数表示相关线段的长度,难度一般.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在
,1.4,-π,3.
,-9中,无理数有( )
| 2 |
| • |
| 2 |
| • |
| 5 |
| A、1个 | B、2个 | C、3个 | D、4个 |
将△ABC向左平移2个单位长度后得到△A′B′C′.若点A的坐标是(-3,7),则点A′的坐标是( )
| A、(-5,5) |
| B、(-1,9) |
| C、(-5,7) |
| D、(-1,7) |
将抛物线y=x2向左平移6个单位,再向下平移8个单位后的抛物线为( )
| A、y=(x+6)2-8 |
| B、y=(x-6)2+8 |
| C、y=(x-6)2-8 |
| D、y=(x+6)2+8 |
在下列函数中,属于二次函数的是( )
A、y=
| ||
B、y=x2+
| ||
| C、y=2x2-1 | ||
D、y=
|
 小猫行走在如图所示的图形上,△ABC顶点是正方形网格中,小猫停留在白砖上的概率为
小猫行走在如图所示的图形上,△ABC顶点是正方形网格中,小猫停留在白砖上的概率为