题目内容
9.计算:1+$\frac{1}{1+2}$+$\frac{1}{1+2+3}$+…+$\frac{1}{1+2+3+…+2005}$.分析 原式利用1+2+3+…+n=$\frac{n(n+1)}{2}$变形,再利用拆项法变形,计算即可得到结果.
解答 解:∵1+2+3+…+n=$\frac{n(n+1)}{2}$,
∴$\frac{1}{1+2+…+n}$=$\frac{2}{n(n+1)}$,
则原式=$\frac{2}{1×2}$+$\frac{2}{2×3}$+$\frac{2}{3×4}$+…+$\frac{2}{2005×2006}$
=2×($\frac{1}{1×2}$+$\frac{1}{2×3}$+…+$\frac{1}{2005×2006}$)
=2×(1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{2005}$-$\frac{1}{2006}$)
=2×(1-$\frac{1}{2006}$)
=$\frac{2005}{1003}$.
点评 此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
19.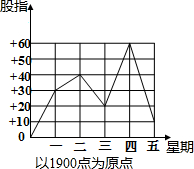 如图为某周上海股市的股指变化折线统计图:
如图为某周上海股市的股指变化折线统计图:
(1)用正数表示比前一天上涨,负数表示比前一天下跌,完成下表:
(2)本周五股指与上周五相比有何变化?变化值是多少?
 如图为某周上海股市的股指变化折线统计图:
如图为某周上海股市的股指变化折线统计图:(1)用正数表示比前一天上涨,负数表示比前一天下跌,完成下表:
| 星期 | 一 | 二 | 三 | 四 | 五 |
| 股指变化(点) | +30 | +10 | -20 | +40 | -50 |
17.下列方程不是一元二次方程的是( )
| A. | 2x2+7=0 | B. | (x+1)(x-1)=0 | C. | 5x2+$\frac{1}{x}$+4=0 | D. | x2=1 |
1.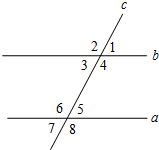 如图,直线a,b都与直线c相交,给出下列条件:
如图,直线a,b都与直线c相交,给出下列条件:
①∠1=∠5;②∠3=∠5;③∠1=∠6;④∠2=∠7;⑤∠4=∠8.
其中,能够得出a∥b的条件是( )
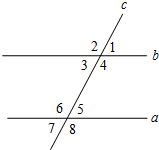 如图,直线a,b都与直线c相交,给出下列条件:
如图,直线a,b都与直线c相交,给出下列条件:①∠1=∠5;②∠3=∠5;③∠1=∠6;④∠2=∠7;⑤∠4=∠8.
其中,能够得出a∥b的条件是( )
| A. | ①②⑤ | B. | ②③⑤ | C. | ③④⑤ | D. | ①②④ |
18.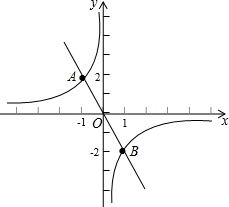 如图,正比例函数y1=kx和反比例函数y2=$\frac{2}{x}$的图象交于A(-1,2)、(1,-2)两点,若y1<y2,则x的取值范围是( )
如图,正比例函数y1=kx和反比例函数y2=$\frac{2}{x}$的图象交于A(-1,2)、(1,-2)两点,若y1<y2,则x的取值范围是( )
 如图,正比例函数y1=kx和反比例函数y2=$\frac{2}{x}$的图象交于A(-1,2)、(1,-2)两点,若y1<y2,则x的取值范围是( )
如图,正比例函数y1=kx和反比例函数y2=$\frac{2}{x}$的图象交于A(-1,2)、(1,-2)两点,若y1<y2,则x的取值范围是( )| A. | x<-1或x>1 | B. | x<-1或0<x<1 | C. | -1<x<0或 0<x<1 | D. | -1<x<0或x>1 |
19.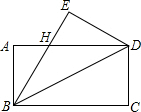 如图,将一块长方形的纸片ABCD沿BD翻折后,点C与E重合,若∠ADB=30°,EH=4cm,则BC的长度为( )
如图,将一块长方形的纸片ABCD沿BD翻折后,点C与E重合,若∠ADB=30°,EH=4cm,则BC的长度为( )
 如图,将一块长方形的纸片ABCD沿BD翻折后,点C与E重合,若∠ADB=30°,EH=4cm,则BC的长度为( )
如图,将一块长方形的纸片ABCD沿BD翻折后,点C与E重合,若∠ADB=30°,EH=4cm,则BC的长度为( )| A. | 10cm | B. | 12cm | C. | 13cm | D. | 14cm |
 如图,将长方形ABCD沿对角线BD折叠后,点C落在C′处,BC′交AD于E,若AD=8,AB=6,则DE=$\frac{25}{4}$.
如图,将长方形ABCD沿对角线BD折叠后,点C落在C′处,BC′交AD于E,若AD=8,AB=6,则DE=$\frac{25}{4}$. 如图所示,有一矩形ABCD,现将其对折,折痕为PQ,再把B点折在折痕线上,得到△ABE,沿着BA线折叠,得到△EAF,△EAF是什么样的三角形?为什么?
如图所示,有一矩形ABCD,现将其对折,折痕为PQ,再把B点折在折痕线上,得到△ABE,沿着BA线折叠,得到△EAF,△EAF是什么样的三角形?为什么?