题目内容
20．
如图，将长方形ABCD沿对角线BD折叠后，点C落在C′处，BC′交AD于E，若AD=8，AB=6，则DE=$\frac{25}{4}$．
分析 根据翻折变换的性质和矩形的性质得到EA=EC′，根据勾股定理得到关于DE的关系式，求出DE的值．
解答 解：∵AD∥BC，
∴∠EDB=∠CBD，又∠EBD=∠CBD，
∴∠EBD=∠EDB，
∴EB=ED，又BC′=BC=AD，
∴EA=EC′，
在Rt△EC′D中，
DE2=EC′2+DC′2，即DE2=（8-DE）2+62，
解得DE=$\frac{25}{4}$．
故答案为：$\frac{25}{4}$．
点评 本题考查的是折叠变换的性质和勾股定理，根据折叠变换的性质找出对应边、对应角是解题的关键．
练习册系列答案
相关题目
15．下列说法正确的是（ ）
| A． | $\frac{8}{27}$的立方根是±$\frac{2}{3}$ | B． | -125没有立方根 | ||
| C． | -1的平方的立方根是1 | D． | $\root{3}{9}$=3 |
5．对于-1来说（ ）
| A． | 有平方根 | B． | 只有算术平方根 | C． | 没有平方根 | D． | 不能确定 |
12．
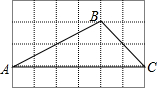如图，△ABC的顶点都是正方形网格中的格点，则sin∠BAC等于（ ）
如图，△ABC的顶点都是正方形网格中的格点，则sin∠BAC等于（ ）| A． | $\frac{\sqrt{2}}{3}$ | B． | $\frac{\sqrt{5}}{5}$ | C． | $\frac{\sqrt{10}}{5}$ | D． | $\frac{1}{3}$ |