题目内容
8.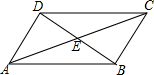 如图,在四边形ABCD中,对角线AC、BD相交于点E,∠CBD=90°,BC=4,BE=ED=3,AC=10,则四边形ABCD的面积为24.
如图,在四边形ABCD中,对角线AC、BD相交于点E,∠CBD=90°,BC=4,BE=ED=3,AC=10,则四边形ABCD的面积为24.
分析 根据勾股定理,可得EC的长,根据平行四边形的判定,可得四边形ABCD的形状,根据平行四边形的面积公式,可得答案.
解答 解:在Rt△BCE中,由勾股定理,得
CE=$\sqrt{B{C}^{2}+B{E}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5.
∵BE=DE=3,AE=CE=5,
∴四边形ABCD是平行四边形.
四边形ABCD的面积为BC•BD=4×(3+3)=24.
故答案为:24.
点评 本题考查了平行四边形的判定与性质,关键是利用勾股定理得出CE的长,利用对角线互相平分的四边形是平行四边形,利用平行四边形的面积公式.

练习册系列答案
相关题目
17.“国庆黄金周”期间,小东和爸爸、妈妈外出旅游,一家三人随机站在一排拍照纪念,小东恰好站在中间的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
18.如果把分式$\frac{2xy}{3x-2y}$中的x和y的值都扩大为原来的2倍,那么分式的值( )
| A. | 扩大为原来的2倍 | B. | 扩大4倍 | C. | 缩小为原来的2倍 | D. | 不变 |
3.观察表格
写出一个y关于x的函数解析式y=1.8x+32.
| x | … | 10 | 20 | 30 | 40 | 50 | … |
| y | … | 50 | 68 | 86 | 104 | 122 | … |
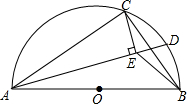 如图,AB是半圆O的直径,点C在半圆O上,AB=5cm,AC=4cm.D是弧BC上的一个动点(含端点B,不含端点C),连接AD,过点C作CE⊥AD于E,连接BE,在点D移动的过程中,BE的取值范围是$\sqrt{13}$-2≤BE<3.
如图,AB是半圆O的直径,点C在半圆O上,AB=5cm,AC=4cm.D是弧BC上的一个动点(含端点B,不含端点C),连接AD,过点C作CE⊥AD于E,连接BE,在点D移动的过程中,BE的取值范围是$\sqrt{13}$-2≤BE<3.