题目内容
15.已知关于x的二元一次方程组$\left\{\begin{array}{l}{2x-3y=0}\\{(k-1)x+(k+1)y=4}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=a}\\{y=b}\end{array}\right.$,且a<0,则k的取值范围是k<$\frac{1}{5}$.分析 先由2x-3y=0得到y=$\frac{2}{3}$x=$\frac{2}{3}a$,与x=a一起代入(k-1)x+(k+1)y=4,求得a,再根据a<0,得到关于k的不等式,解不等式可求k的取值范围.
解答 解:由2x-3y=0得y=$\frac{2}{3}$x=$\frac{2}{3}a$,
与x=a一起代入(k-1)x+(k+1)y=4,
(k-1)a+(k+1)×$\frac{2}{3}a$=4,
解得a=$\frac{12}{5k-1}$,
∵a<0,
∴$\frac{12}{5k-1}$<0,
解得k<$\frac{1}{5}$.
故k的取值范围是k<$\frac{1}{5}$.
故答案为:k<$\frac{1}{5}$.
点评 本题考查了解二元一次方程,解一元一次不等式组,解题的关键是把k看做已知数得到关于k的不等式.

练习册系列答案
相关题目
5.下列各组整式中不是同类项的是( )
| A. | 3m2n与-4nm2 | B. | $\frac{1}{3}$xy2与$\frac{1}{3}$x2y2 | C. | -5ab与2×103ab | D. | 35与-12 |
6.如果公司盈利20万元记作+20万元,那么亏本50万元记作( )
| A. | +50万元 | B. | -50万元 | C. | +20万元 | D. | -20万元 |
3. 如图,将△ABC绕点C顺时针旋转90°后得到△A′B′C′,则点A的对应点A′的坐标为( )
如图,将△ABC绕点C顺时针旋转90°后得到△A′B′C′,则点A的对应点A′的坐标为( )
 如图,将△ABC绕点C顺时针旋转90°后得到△A′B′C′,则点A的对应点A′的坐标为( )
如图,将△ABC绕点C顺时针旋转90°后得到△A′B′C′,则点A的对应点A′的坐标为( )| A. | (0,$\sqrt{2}$) | B. | (0,-3) | C. | (-1,0) | D. | (3,0) |
10.在平面直角坐标系中,点P(-2,3)关于x轴的对称点在( )
| A. | 第四象限 | B. | 第一象限 | C. | 第二象限 | D. | 第三象限 |
 如图,在△ABC中,点O是BC的中点,过点O的直线分别交直线AB,AC于不同的两点
如图,在△ABC中,点O是BC的中点,过点O的直线分别交直线AB,AC于不同的两点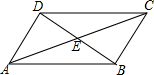 如图,在四边形ABCD中,对角线AC、BD相交于点E,∠CBD=90°,BC=4,BE=ED=3,AC=10,则四边形ABCD的面积为24.
如图,在四边形ABCD中,对角线AC、BD相交于点E,∠CBD=90°,BC=4,BE=ED=3,AC=10,则四边形ABCD的面积为24. 如图是一个正方体纸盒的展开图,当折成纸盒时,与数11重合的数是1和7.
如图是一个正方体纸盒的展开图,当折成纸盒时,与数11重合的数是1和7.