题目内容
20.我们定义:有一组对角相等而另一对角不相等的凸四边形叫做“等对角四边形”.已知:在“等对角四边形”ABCD中,∠DAB=60°,∠ABC=90°,AB=5,AD=4,求对角线AC的长.分析 分两种情况:①当∠ADC=∠ABC=90°时,延长AD,BC相交于点E,先用含30°角的直角三角形的性质求出AE,得出DE,再用三角函数求出CD,由勾股定理求出AC;
②当∠BCD=∠DAB=60°时,过点D作DM⊥AB于点M,DN⊥BC于点N,则∠AMD=90°,四边形BNDM是矩形,先求出AM、DM,再由矩形的性质得出DN=BM=3,BN=DM=2$\sqrt{3}$,求出CN、BC,根据勾股定理求出AC即可.
解答 解:分两种情况:
①当∠ADC=∠ABC=90°时,延长AD,BC相交于点E,如图1所示: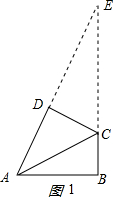
∵∠ABC=90°,∠DAB=60°,AB=5,
∴∠E=30°,
∴AE=2AB=10,
∴DE=AE-AD=10-4═6,
∵∠EDC=90°,∠E=30°,
∴CD=2$\sqrt{3}$,
∴AC=$\sqrt{A{D}^{2}+C{D}^{2}}$=$\sqrt{{4}^{2}+(2\sqrt{3})^{2}}$=2$\sqrt{7}$;
②当∠BCD=∠DAB=60°时,
过点D作DM⊥AB于点M,DN⊥BC于点N,如图2所示: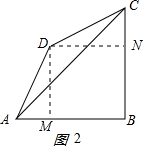
则∠AMD=90°,四边形BNDM是矩形,
∵∠DAB=60°,
∴∠ADM=30°,
∴AM=$\frac{1}{2}$AD=2,
∴DM=2$\sqrt{3}$
∴BM=AB-AM=5-2=3,
∵四边形BNDM是矩形,
∴DN=BM=3,BN=DM=2$\sqrt{3}$,
∵∠BCD=60°,
∴CN=$\sqrt{3}$,
∴BC=CN+BN=3$\sqrt{3}$,
∴AC=$\sqrt{{5}^{2}+(3\sqrt{3})^{2}}$=2$\sqrt{13}$;
综上所述:AC的长为2$\sqrt{7}$或2$\sqrt{13}$.
点评 此题考查了新定义、四边形内角和定理、勾股定理、矩形的判定与性质等知识,需要进行分类讨论,通过作辅助线运用三角函数和勾股定理才能得出结果.

| A. | 40° | B. | 80° | C. | 120° | D. | 160° |
| A. | 第四象限 | B. | 第一象限 | C. | 第二象限 | D. | 第三象限 |
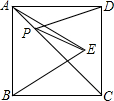 如图,正方形ABCD的边长为2,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE最小,则这个最小值为( )
如图,正方形ABCD的边长为2,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE最小,则这个最小值为( )| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{2}$ | D. | 3 |
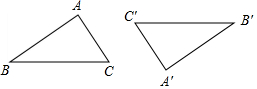 如图,在△ABC与△A′B′C′中,AB=A′B′,∠A=∠A′,要说明△ABC≌△A′B′C′,还需要增加一个条件,下列条件中不符合的是( )
如图,在△ABC与△A′B′C′中,AB=A′B′,∠A=∠A′,要说明△ABC≌△A′B′C′,还需要增加一个条件,下列条件中不符合的是( )| A. | ∠B=∠B′ | B. | ∠C=∠C′ | C. | AC=A′C′ | D. | CB=C′B′ |
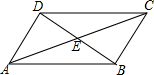 如图,在四边形ABCD中,对角线AC、BD相交于点E,∠CBD=90°,BC=4,BE=ED=3,AC=10,则四边形ABCD的面积为24.
如图,在四边形ABCD中,对角线AC、BD相交于点E,∠CBD=90°,BC=4,BE=ED=3,AC=10,则四边形ABCD的面积为24.