题目内容
13.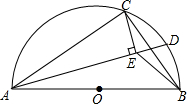 如图,AB是半圆O的直径,点C在半圆O上,AB=5cm,AC=4cm.D是弧BC上的一个动点(含端点B,不含端点C),连接AD,过点C作CE⊥AD于E,连接BE,在点D移动的过程中,BE的取值范围是$\sqrt{13}$-2≤BE<3.
如图,AB是半圆O的直径,点C在半圆O上,AB=5cm,AC=4cm.D是弧BC上的一个动点(含端点B,不含端点C),连接AD,过点C作CE⊥AD于E,连接BE,在点D移动的过程中,BE的取值范围是$\sqrt{13}$-2≤BE<3.
分析 由∠AEC=90°知E在以AC为直径的⊙M的$\widehat{CN}$上(不含点C、可含点N),从而得BE最短时,即为连接BM与⊙M的交点(图中点E′点),作MF⊥AB于F,证△AMF∽△ABC得$\frac{MF}{BC}$=$\frac{AM}{AB}$,即可知MF=$\frac{6}{5}$、AF=$\sqrt{A{M}^{2}-M{F}^{2}}$=$\frac{8}{5}$、BF=$\frac{17}{5}$、BM=$\sqrt{13}$,从而得BE长度的最小值BE′=BM-ME′=$\sqrt{13}$-2;由BE最长时即E与C重合,根据BC=3且点E与点C不重合,得BE<3,从而得出答案.
解答 解:如图,
由题意知,∠AEC=90°,
∴E在以AC为直径的⊙M的$\widehat{CN}$上(不含点C、可含点N),
∴BE最短时,即为连接BM与⊙M的交点(图中点E′点),
∵AB=5,AC=4,
∴BC=3,
作MF⊥AB于F,
∴∠AFM=∠ACB=90°,∠FAM=∠CAB,
∴△AMF∽△ABC,
∴$\frac{MF}{BC}$=$\frac{AM}{AB}$,即$\frac{MF}{3}=\frac{2}{5}$,得MF=$\frac{6}{5}$,
∴AF=$\sqrt{A{M}^{2}-M{F}^{2}}$=$\frac{8}{5}$,
则BF=AB-AF=$\frac{17}{5}$,
∴BM=$\sqrt{M{F}^{2}+B{F}^{2}}$=$\sqrt{13}$,
∴BE长度的最小值BE′=BM-ME′=$\sqrt{13}$-2,
BE最长时,即E与C重合,
∵BC=3,且点E与点C不重合,
∴BE<3,
综上,$\sqrt{13}$-2≤BE<3,
故答案为:$\sqrt{13}$-2≤BE<3.
点评 本题主要考查圆周角定理、勾股定理、相似三角形的判定与性质等知识点,根据题意得出BE最短时,即为连接BM与⊙M的交点是解题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| 身高(cm) | 172 | 173 | 175 | 176 |
| 人数(个) | 4 | 4 | 4 | 4 |
| A. | 173cm,173cm | B. | 174cm,174cm | C. | 173cm,174cm | D. | 174cm,175cm |
 如图,将△ABC绕点C顺时针旋转90°后得到△A′B′C′,则点A的对应点A′的坐标为( )
如图,将△ABC绕点C顺时针旋转90°后得到△A′B′C′,则点A的对应点A′的坐标为( )| A. | (0,$\sqrt{2}$) | B. | (0,-3) | C. | (-1,0) | D. | (3,0) |
 如图,在△ABC中,点O是BC的中点,过点O的直线分别交直线AB,AC于不同的两点
如图,在△ABC中,点O是BC的中点,过点O的直线分别交直线AB,AC于不同的两点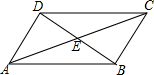 如图,在四边形ABCD中,对角线AC、BD相交于点E,∠CBD=90°,BC=4,BE=ED=3,AC=10,则四边形ABCD的面积为24.
如图,在四边形ABCD中,对角线AC、BD相交于点E,∠CBD=90°,BC=4,BE=ED=3,AC=10,则四边形ABCD的面积为24. 为了响应国家节能减排的号召,鼓励市民节约用电,我市从2016年7月1日起,居民用电实行“一户一表”的“阶梯电价”,分三个档次收费,第一档是用电量不超过180千瓦时实行“基本电价”,第二、三档实行“提高电价”,具体收费情况见折线图,请根据图象回答下列问题:
为了响应国家节能减排的号召,鼓励市民节约用电,我市从2016年7月1日起,居民用电实行“一户一表”的“阶梯电价”,分三个档次收费,第一档是用电量不超过180千瓦时实行“基本电价”,第二、三档实行“提高电价”,具体收费情况见折线图,请根据图象回答下列问题: