题目内容
16.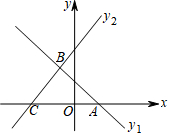 如图,在平面直角坐标系xOy中,直线y1=-x+b过点A,且与直线y2=x+3相交于点B(m,2),直线y2=x+3与x轴相交于点C.
如图,在平面直角坐标系xOy中,直线y1=-x+b过点A,且与直线y2=x+3相交于点B(m,2),直线y2=x+3与x轴相交于点C.(1)求m的值.
(2)求△ABC的面积.
(3)根据图象,直接写出关于x的不等式-x+b>x+3的解集.
分析 (1)由点B的坐标利用一次函数图象上点的坐标特征可求出m值;
(2)由点B的坐标利用一次函数图象上点的坐标特征可求出b的值,再利用一次函数图象上点的坐标特征可求出点A、C的值,由点A、B、C的坐标利用三角形的面积可求出△ABC的面积;
(3)根据两直线的上下位置关系结合点B的横坐标,即可得出不等式的解集.
解答 解:(1)∵直线y2=x+3过点B(m,2),
∴2=m+3,
解得:m=-1.
(2)∵直线y1=-x+b过点B(-1,2),
∴2=1+b,
解得:b=1,
∴直线y1的解析式为y1=-x+1.
当y1=-x+1=0时,x=1,
∴点A的坐标为(1,0);
当y2=x+3=0时,x=-3,
∴点C的坐标为(-3,0),
∴BC=1-(-3)=4,
∴S△ABC=$\frac{1}{2}$AC•yB=$\frac{1}{2}$×4×2=4.
(3)观察函数图象,可知:当x<-1时,直线y1在直线y2的上方,
∴不等式-x+b>x+3的解集为x<-1.
点评 本题考查了一次函数与一元一次不等式、一次函数图象上点的坐标特征以及三角形的面积,解题的关键是:(1)将y2=2代入y2=x+3中求出x值;(2)利用一次函数图象上点的坐标特征求出点A、C的坐标;(3)由两直线的上下位置关系找出不等式的解集.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案
相关题目
4.下列不等式中一定成立的是( )
| A. | 5a>4a | B. | -a>-2a | C. | a+2<a+3 | D. | $\frac{2}{a}$<$\frac{3}{a}$ |
1.下表是某校八年级(1)班43名学生右眼视力的检查结果.
(1)该班学生右眼视力的平均数是4.6(结果保留1位小数).
(2)该班学生右眼视力的中位数是4.7.
(3)该班小鸣同学右眼视力是4.5,能不能说小鸣同学的右眼视力处于全班同学的中上水平?试说明理由.
| 视力 | 4.0 | 4.1 | 4.2 | 4.3 | 4.4 | 4.5 | 4.6 | 4.7 | 4.8 | 4.9 | 5.0 |
| 人数 | 1 | 2 | 5 | 4 | 3 | 5 | 1 | 1 | 5 | 10 | 6 |
(2)该班学生右眼视力的中位数是4.7.
(3)该班小鸣同学右眼视力是4.5,能不能说小鸣同学的右眼视力处于全班同学的中上水平?试说明理由.
8.在下列四项调查中,方式正确的是( )
| A. | 了解本市中学生每天学习所用的时间,采用全面调查的方式 | |
| B. | 为保证运载火箭的成功发射,对其所有的零部件采用抽样调查的方式 | |
| C. | 了解某市每天的流动人口数,采用全面调查的方式 | |
| D. | 了解全市中学生的视力情况,采用抽样调查的方式 |
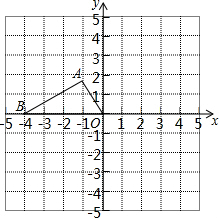 如图,A、B两点的坐标分别是A (-1,$\sqrt{3}$),B (-3,0)
如图,A、B两点的坐标分别是A (-1,$\sqrt{3}$),B (-3,0)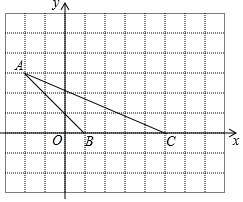 如图所示,小方格边长为1个单位,
如图所示,小方格边长为1个单位,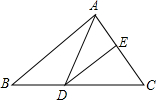 如图,DE是△ABC中AC边的垂直平分线,若AB=7cm,BC=10cm,则△ABD的周长为17cm.
如图,DE是△ABC中AC边的垂直平分线,若AB=7cm,BC=10cm,则△ABD的周长为17cm.