Question

11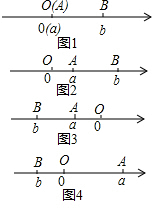．（1）阅读下面材料：点A、B在数轴上分别表示实数a、b，A、B两点之间的距离表示为|AB|．当A、B两点中有一点在原点时，不妨设点A在原点，如图1，|AB|=|OB|=|b|=|a-b|，当A、B两点都不在原点时，
①如图2，点A、B都在原点的右边，|AB|=|OB|-|OA|=|b|-|a|=b-a=|a-b|；
②如图3，点A、B都在原点的左边，|AB|=|OB|-|OA|=|b|-|a|=（-b）-（-a）=a-b=|a-b|；
③如图4，点A、B在原点的两边，|AB|=|OB|+|OA|=|b|+|a|=（-b）+a=a-b=|a-b|；
综上，数轴上A、B两点之间的距离|AB|=|a-b|．
（2）回答下列问题：
①数轴上表示1005和-1011的两点之间的距离是2016；
②数轴上分别表示x、-5的两点A、B之间的距离是|x+5|，如果|AB|=2，那么x为-3或-7；
③若|x+3|＞|x-5|，则相应x的取值范围是x＞1；
④代数式|x+2|+|x-3|+|x-1|的最小值为5．

Answer 1

分析 ①根据两点间距离公式计算即可．
②根据两点间距离公式计算，把问题转化为方程解决．
③当x≤-3时，无解．当-3＜x＜5时，1＜x＜5，当x≥5时，不等式恒成立，由此即可解决问题．
④求代数式|x+2|+|x-3|+|x-1|的最小值就是在数轴上找一点P到表示-2，1，3的点的距离之和最小，当P与表示1的点重合时，点P到表示-2，1，3的点的距离之和最小．

解答 解：①数轴上表示1005和-1011的两点之间的距离是|1005-（-1011）|=2016，
故答案为：2016；

②数轴上分别表示x、-5的两点A、B之间的距离是|x+5|，
∵|AB|=2，
∴|x+5|=2，
解得：x=-3或-7，
故答案为：|x+5|，-3或-7；

③|x+3|＞|x-5|，则相应x的取值范围是：
当x≤-3时，无解．
当-3＜x＜5时，1＜x＜5，
当x≥5时，不等式恒成立，
综上所述，x的取值范围为x＞1．
故答案为x＞1．

④代数式|x+2|+|x-3|+|x-1|的最小值为，
求代数式|x+2|+|x-3|+|x-1|的最小值就是在数轴上找一点P到表示-2，1，3的点的距离之和最小，当P与表示1的点重合时，点P到表示-2，1，3的点的距离之和最小，最小值为5．
故答案为5．

点评 本题考查实数与数轴、绝对值．两点间距离公式等知识，解题的关键是理解题意，把问题转化为方程解决，学会用绝对值的几何意义解决实际问题，属于中考常考题型．