题目内容
 直线y=
直线y=| 2 |
| 3 |
| k |
| x |
(1)求△AOB的面积;
(2)求反比例函数关系式;
(3)过△AOC的顶点能不能画出直线把△AOC分成面积相等的两部分?若能,可以画出几条?写出其中一条直线所对应的函数关系式.
考点:反比例函数与一次函数的交点问题
专题:计算题
分析:(1)根据坐标轴上点的坐标特征求出B点坐标为(0,-2);点A的坐标为(3,0),然后根据三角形面积公式求解;
(2)先利用直线解析式求出C点坐标,然后根据反比例函数图象上点的坐标特征求出k的值即可得到反比例函数解析式;
(3)根据三角形面积公式,取各边的中点,则三条中线所在的性质能把△AOC分成面积相等的两部分,然后根据线段中点公式求出三边中点坐标,再利用待定系数法分别求出三条直线的解析式.
(2)先利用直线解析式求出C点坐标,然后根据反比例函数图象上点的坐标特征求出k的值即可得到反比例函数解析式;
(3)根据三角形面积公式,取各边的中点,则三条中线所在的性质能把△AOC分成面积相等的两部分,然后根据线段中点公式求出三边中点坐标,再利用待定系数法分别求出三条直线的解析式.
解答:解:(1)当y=0时,y=
x-2=-2,则B点坐标为(0,-2);
当x=0时,
x-2=0,解得x=3,则点A的坐标为(3,0),
所以△AOB的面积=
×2×3=3;
(2)把C(a,2)代入y=
x-2得
a-2=2,解得a=6,
所以C点坐标为(6,2),
因为C(6,2)在反比例函数y=
的图象上,
所以k=6×2=12,
所以反比例函数解析式为y=
;
(3)能,可以画三条.
设OC的中点为D,则直线AD把△AOC分成面积相等的两部分,D点坐标为(3,1),直线AD的解析式为x=3;
设OA的中点为E,则直线CE把△AOC分成面积相等的两部分,E点坐标为(
,0),直线CE的解析式为y=
x-
;
设AC的中点为F,则直线OF把△AOC分成面积相等的两部分,F点坐标为(
,1),直线OF的解析式为y=
x.
| 2 |
| 3 |
当x=0时,
| 2 |
| 3 |
所以△AOB的面积=
| 1 |
| 2 |
(2)把C(a,2)代入y=
| 2 |
| 3 |
| 2 |
| 3 |
所以C点坐标为(6,2),
因为C(6,2)在反比例函数y=
| k |
| x |
所以k=6×2=12,
所以反比例函数解析式为y=
| 12 |
| x |
(3)能,可以画三条.
设OC的中点为D,则直线AD把△AOC分成面积相等的两部分,D点坐标为(3,1),直线AD的解析式为x=3;
设OA的中点为E,则直线CE把△AOC分成面积相等的两部分,E点坐标为(
| 3 |
| 2 |
| 4 |
| 9 |
| 2 |
| 3 |
设AC的中点为F,则直线OF把△AOC分成面积相等的两部分,F点坐标为(
| 9 |
| 2 |
| 2 |
| 9 |
点评:本题考查了反比例函数与一次函数的交点问题:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.

练习册系列答案
相关题目
 下列对于如图所示直线的表示,其中正确的是( )
下列对于如图所示直线的表示,其中正确的是( )①直线A ②直线b ③直线AB ④直线Ab ⑤直线Bb.
| A、①③ | B、②③ | C、③④ | D、②⑤ |
抛物线y=-2x2-4x-5经过平移得到y=-2x2,平移方法是( )
| A、向左平移1个单位,再向下平移3个单位 |
| B、向左平移1个单位,再向上平移3个单位 |
| C、向右平移1个单位,再向下平移3个单位 |
| D、向右平移1个单位,再向上平移3个单位 |
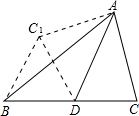 如图,AD是△ABC的中线,∠ADC=60°,△ADC沿直线AD解析,点C落在点C1的位置,如果DC=2,那么BC1的值为( )
如图,AD是△ABC的中线,∠ADC=60°,△ADC沿直线AD解析,点C落在点C1的位置,如果DC=2,那么BC1的值为( ) 如图,直线AB,CD相交于点O,过点O画射线OE,若OB平分∠DOE,∠2:∠3=2:5,求∠AOD与∠AOC的度数.
如图,直线AB,CD相交于点O,过点O画射线OE,若OB平分∠DOE,∠2:∠3=2:5,求∠AOD与∠AOC的度数. “汶川”地震后,成都乙粮库以每天相同的速度将粮食运往灾区,为缓解成都乙粮库的压力,河南省甲粮库以汽车运输的方式予以支援,如图是两粮库的储粮量y(万吨)与时间x(天)之间的函数图象,在单位时间内甲粮库的出粮量与乙粮库的进粮量是相同的(不考虑粮食的损耗),通过图象回答下列问题.
“汶川”地震后,成都乙粮库以每天相同的速度将粮食运往灾区,为缓解成都乙粮库的压力,河南省甲粮库以汽车运输的方式予以支援,如图是两粮库的储粮量y(万吨)与时间x(天)之间的函数图象,在单位时间内甲粮库的出粮量与乙粮库的进粮量是相同的(不考虑粮食的损耗),通过图象回答下列问题.