题目内容
13.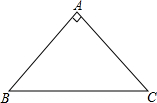 知图,△ABC中,AB=AC,∠A=90°.
知图,△ABC中,AB=AC,∠A=90°.(1)在图中作△ABC的角平分线BD(要求保留作图痕迹);
(2)请说明:AB+AD=BC.
分析 (1)首先以B为圆心,任意长为半径画弧,交AB、BC与M、N,再以M、N为圆心,大于$\frac{1}{2}$MN长为半径画弧,两弧交于点K,再画射线BK交AC于D,BD就是△ABC的角平分线BD;
(2)过D作DE⊥BC于E,根据角平分线性质求出AD=DE,推出AB=BE,求出∠C=∠EDC,推出AD=DE=CE,代入求出即可.
解答 
 解:(1)如图所示:
解:(1)如图所示:
(2).证明:过D作DE⊥BC于E,
∵BD平分∠ABC,DE⊥BC,∠DAB=90°,
∴AD=DE,
由勾股定理得:AB2=BD2-AD2,BE2=BD2-DE2,
∴AB=BE,
∵∠A=90°,AC=AB,
∴∠C=∠ABC=$\frac{1}{2}$(180°-90°)=45°,
∵DE⊥BC,
∴∠DEC=90°,
∴∠EDC=180°-90°-45°=45°=∠C,
∴DE=EC,
∴BC=BE+CE=AB+AD.
点评 此题主要考查了基本作图,以及角平分线的性质,关键是正确画出图形,掌握角的平分线上的点到角的两边的距离相等.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
 如图,在△ABC中,已知点D、E、F分别为边BC、AD、CE的中点,若△ABC的面积为16,则图中阴影部分的面积为4.
如图,在△ABC中,已知点D、E、F分别为边BC、AD、CE的中点,若△ABC的面积为16,则图中阴影部分的面积为4. 如图,AD是△ABC的角平分线,P是AD延长线上一点,PM∥AC交BC于M,PN∥AB交BC于N.求证:点D到PM、PN的距离相等.
如图,AD是△ABC的角平分线,P是AD延长线上一点,PM∥AC交BC于M,PN∥AB交BC于N.求证:点D到PM、PN的距离相等.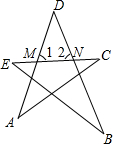 如图,图形ABCDE是五星形,∠1是△ACM的外角,那么∠1等于哪两个内角的和?∠2是△BEN的外角,那么∠2等于哪两个内角的和?由此可知∠A+∠B+∠C+∠D+∠E的和是多少度?
如图,图形ABCDE是五星形,∠1是△ACM的外角,那么∠1等于哪两个内角的和?∠2是△BEN的外角,那么∠2等于哪两个内角的和?由此可知∠A+∠B+∠C+∠D+∠E的和是多少度?