题目内容
3.观察下列算式,寻找规律,利用规律解答后面的问题:1×3+1=4=22,2×4+1=9=32,3×5+1=16=42,4×6+1=25=52,…
(1)计算:7×9+1=64=(8)2;
(2)请你用找到的规律计算:(1+$\frac{1}{1×3}$)×$(1+\frac{1}{2×4})$×$(1+\frac{1}{3×5})$×$…×(1+\frac{1}{9×11})$.
分析 (1)观察发现一个正整数乘以比这个正整数大2的数再加1就等于这个正整数加1的平方,依此得到7×9+1=64=82;
(2)由1+$\frac{1}{n(n+2)}$)=$\frac{n+1}{n}$×$\frac{n+1}{n+2}$,将原式变形为$\frac{2}{1}$×$\frac{2}{3}$×$\frac{3}{2}$×$\frac{3}{4}$×$\frac{4}{3}$×$\frac{4}{5}$×…×$\frac{10}{9}$×$\frac{10}{11}$,再约分计算即可求解.
解答 解:(1)7×9+1=64=82;
(2)(1+$\frac{1}{1×3}$)×$(1+\frac{1}{2×4})$×$(1+\frac{1}{3×5})$×$…×(1+\frac{1}{9×11})$
=$\frac{2}{1}$×$\frac{2}{3}$×$\frac{3}{2}$×$\frac{3}{4}$×$\frac{4}{3}$×$\frac{4}{5}$×…×$\frac{10}{9}$×$\frac{10}{11}$
=$\frac{2×10}{11}$
=$\frac{20}{11}$.
故答案为:8.
点评 本题考查了有理数的运算,是找规律题,找到(1+$\frac{1}{1×3}$)×$(1+\frac{1}{2×4})$×$(1+\frac{1}{3×5})$×…×(1+$\frac{1}{n(n+2)}$)=$\frac{2}{1}$×$\frac{2}{3}$×$\frac{3}{2}$×$\frac{3}{4}$×$\frac{4}{3}$×$\frac{4}{5}$×…×$\frac{n+1}{n}$×$\frac{n+1}{n+2}$=$\frac{2(n+1)}{n+2}$是解题的关键.

 知图,△ABC中,AB=AC,∠A=90°.
知图,△ABC中,AB=AC,∠A=90°.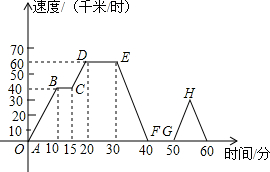 星期天到外婆家去,他记录了汽车行驶的速度随时间的变化情况,到了外婆家画出如图所示的图象
星期天到外婆家去,他记录了汽车行驶的速度随时间的变化情况,到了外婆家画出如图所示的图象