题目内容
8.计算:1$\frac{1}{2}$-2$\frac{5}{6}$+3$\frac{1}{12}$-4$\frac{19}{20}$+5$\frac{1}{30}$-6$\frac{41}{42}$.分析 将式子变形为1+$\frac{1}{2}$-3+$\frac{1}{6}$+3+$\frac{1}{12}$-5+$\frac{1}{20}$+5+$\frac{1}{30}$-7+$\frac{1}{42}$,再拆分抵消即可求解.
解答 解:1$\frac{1}{2}$-2$\frac{5}{6}$+3$\frac{1}{12}$-4$\frac{19}{20}$+5$\frac{1}{30}$-6$\frac{41}{42}$
=1+$\frac{1}{2}$-3+$\frac{1}{6}$+3+$\frac{1}{12}$-5+$\frac{1}{20}$+5+$\frac{1}{30}$-7+$\frac{1}{42}$
=(1-3+3-5+5-7)+(1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+$\frac{1}{4}$-$\frac{1}{5}$+$\frac{1}{5}$-$\frac{1}{6}$+$\frac{1}{6}$-$\frac{1}{7}$)
=-6+(1-$\frac{1}{7}$)
=-5$\frac{1}{7}$.
点评 考查了有理数的加减混合运算,注意
①在一个式子里,有加法也有减法,根据有理数减法法则,把减法都转化成加法,并写成省略括号的和的形式.
②转化成省略括号的代数和的形式,就可以应用加法的运算律,使计算简化.

练习册系列答案
相关题目
17.对于抛物线y=-x2+2x-3,下列结论正确的是( )
| A. | 与x轴有两个交点 | B. | 开口向上 | ||
| C. | 与y轴的交点坐标是(0,3) | D. | 当x=1时,y有最大值为-2 |
 如图,在Rt△ABC中,∠ACB=90°,∠CAB的角平分线AF与AB上的高CD相交于点E,△CEF是等腰三角形吗?为什么?
如图,在Rt△ABC中,∠ACB=90°,∠CAB的角平分线AF与AB上的高CD相交于点E,△CEF是等腰三角形吗?为什么?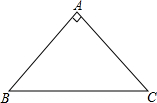 知图,△ABC中,AB=AC,∠A=90°.
知图,△ABC中,AB=AC,∠A=90°.