题目内容
1.无论x、y取任何值,多边形x2+y2-2x-4y+6的值总是( )| A. | 正数 | B. | 负数 | C. | 非正数 | D. | 非负数 |
分析 利用完全平方公式把多项式分组配方变形后,利用非负数的性质判断即可.
解答 解:∵x2+y2-2x-4y+6=(x2-2x+1)+(y2-4y+4)+1=(x-1)2+(y-2)2+1≥1>0,
∴多项式的值总是正数.
故选:A.
点评 此题考查了配方法的应用,以及非负数的性质,利用完全平方公式分组分解是解决问题的关键.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案
相关题目
12.已知实数a,b,c均不为零,且满足a+b+c=0,则$\frac{1}{{b}^{2}+{c}^{2}-{a}^{2}}$+$\frac{1}{{c}^{2}+{a}^{2}-{b}^{2}}$+$\frac{1}{{a}^{2}+{b}^{2}-{c}^{2}}$的值是( )
| A. | 为正 | B. | 为负 | ||
| C. | 为0 | D. | 与a,b,c的取值有关 |
10.化简$\frac{x-2}{x+2}+\frac{x+2}{2-x}$的结果是( )
| A. | $\frac{-8x}{{x}^{2}-4}$ | B. | $\frac{-8x}{{x}^{2}+4}$ | C. | $\frac{8x}{{x}^{2}-4}$ | D. | $\frac{2{x}^{2}+8}{{x}^{2}-4}$ |
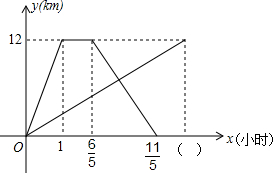 一条笔直的公路连通A、B两地.甲、乙两人同时从A地前往B地,甲骑自行车,乙步行.甲到达B地并在B地停留12分钟后,再按原路原速返回.当甲返回到A地时,乙距B地1千米,他们各自距A地的距离y(千米)与乙步行时间x(小时)之间的函数图象如图所示.请结合图象信息解答下列问题:
一条笔直的公路连通A、B两地.甲、乙两人同时从A地前往B地,甲骑自行车,乙步行.甲到达B地并在B地停留12分钟后,再按原路原速返回.当甲返回到A地时,乙距B地1千米,他们各自距A地的距离y(千米)与乙步行时间x(小时)之间的函数图象如图所示.请结合图象信息解答下列问题: