题目内容
17.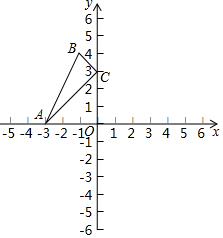 已知点A(-3,0),点C(0,3)且点B的坐标为(-1,4),计算△ABC的面积.
已知点A(-3,0),点C(0,3)且点B的坐标为(-1,4),计算△ABC的面积.
分析 过点B作BD⊥y轴于点D,利用梯形和三角形的面积公式结合S△ABC=S梯形AODB-S△AOC-S△BCD即可求出△ABC的面积.
解答 解:过点B作BD⊥y轴于点D,如图所示.
∵点B的坐标为(-1,4),
∴点D(0,4),
∴BD=1,OD=4.
∵点A(-3,0),点C(0,3),
∴AO=3,CD=1,OC=3,
∴S△ABC=S梯形AODB-S△AOC-S△BCD
=$\frac{1}{2}$(AO+BD)•OD-$\frac{1}{2}$AO•OC-$\frac{1}{2}$BD•CD
=3.
点评 本题考查坐标与图形性质、梯形的面积以及三角形的面积,根据分割图形求面积法找出S△ABC=S梯形AODB-S△AOC-S△BCD是解题的关键.

练习册系列答案
相关题目
12.直线y=x+3上有一点P(3,n),则点P关于原点的对称点P′的坐标是( )
| A. | (-3,-6) | B. | (-6,3) | C. | (6,3) | D. | (-6,-3) |
 如图,直角坐标平面内有两点A($\sqrt{3}$,1),B(1,$1\sqrt{3}$),将△AOB绕点O逆时针方向旋转150°得到△A′OB′,则线段AB的中点M所经过的路线长为$\frac{5\sqrt{6}+5\sqrt{2}}{12}$π.
如图,直角坐标平面内有两点A($\sqrt{3}$,1),B(1,$1\sqrt{3}$),将△AOB绕点O逆时针方向旋转150°得到△A′OB′,则线段AB的中点M所经过的路线长为$\frac{5\sqrt{6}+5\sqrt{2}}{12}$π.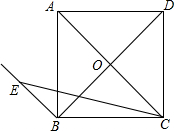 如图,四边形ABCD为正方形,EB∥AC,EC=AC,E在FB上,求∠ECB的度数.
如图,四边形ABCD为正方形,EB∥AC,EC=AC,E在FB上,求∠ECB的度数.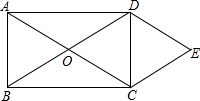 如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD.
如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD.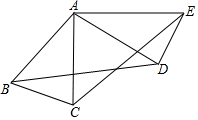 如图,△ABC中,AB=AC,∠ABC=70°.△ABC绕点A按逆时针方向旋转一定角度后,得到△ADE.问:
如图,△ABC中,AB=AC,∠ABC=70°.△ABC绕点A按逆时针方向旋转一定角度后,得到△ADE.问: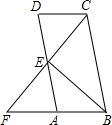 如图,在?ABCD中,BC=2CD,E为AD的中点,CE,BA的延长线交于点F,求证:∠F=∠BCF.
如图,在?ABCD中,BC=2CD,E为AD的中点,CE,BA的延长线交于点F,求证:∠F=∠BCF.