题目内容
 等腰△ABC内接于⊙O,AB=AC=10,cosB=
等腰△ABC内接于⊙O,AB=AC=10,cosB=| 3 |
| 5 |
考点:三角形的内切圆与内心
专题:
分析:根据等腰三角形的性质得出AE⊥BC,进而得出AE过点I,求出BF的长,即可利用勾股定理得出FI以及BI的长.
解答: 解:连接AO并延长到BC于点E,过点I作IF⊥AB于点F,
解:连接AO并延长到BC于点E,过点I作IF⊥AB于点F,
∵等腰△ABC内接于⊙O,AB=AC=10,
∴AE⊥BC,
∵cosB=
,AB=AC=10,
∴BE=6,AE=8,
∵AE⊥BC,AB=AC,
∴∠BAE=∠CAE,
∵I为△ABC的内心,∠ABI=∠EBI,
∴AE过点I,
∵IF⊥AB,IE⊥BC,∠ABI=∠EBI,
∴IF=IE,
在Rt△BEI和Rt△BFI中,
,
∴Rt△BEI≌Rt△BFI(HL),
∴BE=BF=6,
∴AF=10-6=4,
设IE=x,则FI=x,AI=8-x,
在Rt△AFI中,
AF2+FI2=AI2,
∴42+x2=(8-x)2,
解得:x=3,
在Rt△AFI中,
BI=
=3
.
故答案为:3
.
 解:连接AO并延长到BC于点E,过点I作IF⊥AB于点F,
解:连接AO并延长到BC于点E,过点I作IF⊥AB于点F,∵等腰△ABC内接于⊙O,AB=AC=10,
∴AE⊥BC,
∵cosB=
| 3 |
| 5 |
∴BE=6,AE=8,
∵AE⊥BC,AB=AC,
∴∠BAE=∠CAE,
∵I为△ABC的内心,∠ABI=∠EBI,
∴AE过点I,
∵IF⊥AB,IE⊥BC,∠ABI=∠EBI,
∴IF=IE,
在Rt△BEI和Rt△BFI中,
|
∴Rt△BEI≌Rt△BFI(HL),
∴BE=BF=6,
∴AF=10-6=4,
设IE=x,则FI=x,AI=8-x,
在Rt△AFI中,
AF2+FI2=AI2,
∴42+x2=(8-x)2,
解得:x=3,
在Rt△AFI中,
BI=
| 62+32 |
| 5 |
故答案为:3
| 5 |
点评:此题主要考查了勾股定理以及三角形内心的性质和全等三角形的判定与性质等知识,得出AE过点I是解题关键.

练习册系列答案
相关题目
 如图,竖直放置的圆柱体的左视图是( )
如图,竖直放置的圆柱体的左视图是( )| A、长方形 | B、等腰梯形 |
| C、等腰三角形 | D、正方形 |
 已知抛物线y=-x2+1的顶点为P,点A是第一象限内该二次函数图象上一点,过点A作x轴的平行线交二次函数图象于点B,分别过点B、A作x轴的垂线,垂足分别为C、D,连结PA、PD,PD交AB于点E,△PAD与△PEA相似吗?( )
已知抛物线y=-x2+1的顶点为P,点A是第一象限内该二次函数图象上一点,过点A作x轴的平行线交二次函数图象于点B,分别过点B、A作x轴的垂线,垂足分别为C、D,连结PA、PD,PD交AB于点E,△PAD与△PEA相似吗?( )| A、始终不相似 |
| B、始终相似 |
| C、只有AB=AD时相似 |
| D、无法确定 |

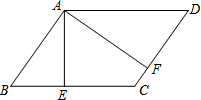 如图,在平行四边形ABCD中,AE⊥BC于E,AF⊥CD于F.
如图,在平行四边形ABCD中,AE⊥BC于E,AF⊥CD于F. 如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,D是边AB上一点,联结CD,把△ACD沿CD所在的直线翻折,点A落在点E的位置,如果DE∥BC,那么AD的长为
如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,D是边AB上一点,联结CD,把△ACD沿CD所在的直线翻折,点A落在点E的位置,如果DE∥BC,那么AD的长为