题目内容
在Rt△ABC中,AB=BC,∠B=90°,将一块等腰直角三角板的直角顶点O放在斜边AC上,将三角板绕点O旋转.

(1)当点O为AC中点时,
①如图1,三角板的两直角边分别交AB,BC于E、F两点,连接EF,猜想线段AE、CF与EF之间存在的等量关系(无需证明);
②如图2,三角板的两直角边分别交AB,BC延长线于E、F两点,连接EF,判断①中的猜想是否成立?若成立,请证明;若不成立,请说明理由;
(2)当点O不是AC中点时,如图3,三角板的两直角边分别交AB,BC于E、F两点,若
=
,求
的值.

(1)当点O为AC中点时,
①如图1,三角板的两直角边分别交AB,BC于E、F两点,连接EF,猜想线段AE、CF与EF之间存在的等量关系(无需证明);
②如图2,三角板的两直角边分别交AB,BC延长线于E、F两点,连接EF,判断①中的猜想是否成立?若成立,请证明;若不成立,请说明理由;
(2)当点O不是AC中点时,如图3,三角板的两直角边分别交AB,BC于E、F两点,若
| AO |
| AC |
| 1 |
| 4 |
| OE |
| OF |
考点:相似形综合题
专题:
分析:(1)①猜想:AE2+CF2=EF2,连接OB,证△OEB≌△OFC,推出BE=CF即可;
②成立.连结OB,求出OB=
,∠BOC=90°,∠EOB=∠FOC,∠EBO=∠FCO,证△OEB≌△OFC,推出BE=CF,在Rt△EBF中,由勾股定理得出BF2+BE2=EF2,即可得出答案;
(2)过点O作OM⊥AB于M,ON⊥BC于N,证△OME∽△ONF,推出
=
,证△AOM∽△OCN,得出比例式,即可得出答案.
②成立.连结OB,求出OB=
| 1 |
| 2 |
(2)过点O作OM⊥AB于M,ON⊥BC于N,证△OME∽△ONF,推出
| OM |
| ON |
| OE |
| OF |
解答:解:(1)①猜想:AE2+CF2=EF2.
②成立.
证明:连结OB.
 ∵AB=BC,∠ABC=90°,O点为AC的中点,
∵AB=BC,∠ABC=90°,O点为AC的中点,
∴OB=
,∠BOC=90°,∠ABO=∠BCO=45°.
∵∠EOF=90°,
∴∠EOB=∠FOC,
又∵∠EBO=∠FCO,
在△OEB和△OFC中
,
∴△OEB≌△OFC,
∴BE=CF,
又∵BA=BC,
∴AE=BF.
在Rt△EBF中,
∵∠EBF=90°,
∴BF2+BE2=EF2,
∴AE2+CF2=EF2.
(2)如图,过点O作OM⊥AB于M,ON⊥BC于N.
∵∠B=90°,
∴∠MON=90°,
∵∠EOF=90°,
∴∠EOM=∠FON.
∵∠EMO=∠FNO=90°,
∴△OME∽△ONF,
∴
=
,
∵△AOM和△OCN为等腰直角三角形,
∴△AOM∽△OCN,
∴
=
,
∵
=
,
∴
=
.
②成立.
证明:连结OB.
 ∵AB=BC,∠ABC=90°,O点为AC的中点,
∵AB=BC,∠ABC=90°,O点为AC的中点,∴OB=
| 1 |
| 2 |
∵∠EOF=90°,
∴∠EOB=∠FOC,
又∵∠EBO=∠FCO,
在△OEB和△OFC中
|
∴△OEB≌△OFC,
∴BE=CF,
又∵BA=BC,
∴AE=BF.
在Rt△EBF中,
∵∠EBF=90°,
∴BF2+BE2=EF2,
∴AE2+CF2=EF2.
(2)如图,过点O作OM⊥AB于M,ON⊥BC于N.
∵∠B=90°,
∴∠MON=90°,
∵∠EOF=90°,
∴∠EOM=∠FON.

∵∠EMO=∠FNO=90°,
∴△OME∽△ONF,
∴
| OM |
| ON |
| OE |
| OF |
∵△AOM和△OCN为等腰直角三角形,
∴△AOM∽△OCN,
∴
| OM |
| ON |
| AO |
| OC |
∵
| AO |
| AC |
| 1 |
| 4 |
∴
| OE |
| OF |
| 1 |
| 3 |
点评:本题考查了相似形的综合,用到的知识点是等腰直角三角形性质,相似三角形的性质和判定,全等三角形的性质和判定的应用,关键是运用数形结合思想,做出辅助线.

练习册系列答案
相关题目
下列语句是命题的是( )
| A、延长线段AB到C |
| B、用量角器画∠AOB=90° |
| C、两点之间线段最短 |
| D、任何数的平方都不小于0吗? |
已知x2-(m-1)x-(2m-2)=0两根之和等于两根之积,则m的值为( )
| A、1 | B、-1 | C、2 | D、-2 |
 如图,点B在点A北偏东50°方向,点C在点B北偏西40°方向,BC=10m,则点C到直线AB的距离为
如图,点B在点A北偏东50°方向,点C在点B北偏西40°方向,BC=10m,则点C到直线AB的距离为 如图,“五一”节,小明和同学一起到游乐场游玩,游乐场的大型摩天轮的半径为20米,旋转1周需要24分钟(匀速).小明乘坐最底部的车厢按逆时针方向旋转(离地面约1米)开始1周的观光.
如图,“五一”节,小明和同学一起到游乐场游玩,游乐场的大型摩天轮的半径为20米,旋转1周需要24分钟(匀速).小明乘坐最底部的车厢按逆时针方向旋转(离地面约1米)开始1周的观光.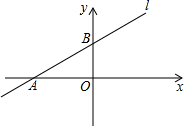 如图,直线l交x轴的负半轴于点A,交y轴的正半轴于点B,线段OA、OB的长分别是方程x2-14x+48=0(OA>OB)的两根的
如图,直线l交x轴的负半轴于点A,交y轴的正半轴于点B,线段OA、OB的长分别是方程x2-14x+48=0(OA>OB)的两根的 如图,AB是圆O的直径,CD⊥AB于D点,AD=4cm,DB=9cm,求CB的长.
如图,AB是圆O的直径,CD⊥AB于D点,AD=4cm,DB=9cm,求CB的长. 已知:如图,AB是⊙O的直径,C是⊙O上一点,OD⊥AC于点D,过点C作⊙O的切线,交OD的延长线于点E,连接AE.
已知:如图,AB是⊙O的直径,C是⊙O上一点,OD⊥AC于点D,过点C作⊙O的切线,交OD的延长线于点E,连接AE.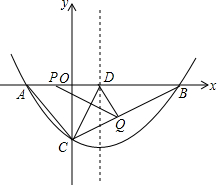 已知抛物线 y=ax2+bx+c(a>0)的图象经过过点B(12,0)和C(0,6),对称轴方程为x=2.
已知抛物线 y=ax2+bx+c(a>0)的图象经过过点B(12,0)和C(0,6),对称轴方程为x=2.