题目内容
 已知:如图,AB是⊙O的直径,C是⊙O上一点,OD⊥AC于点D,过点C作⊙O的切线,交OD的延长线于点E,连接AE.
已知:如图,AB是⊙O的直径,C是⊙O上一点,OD⊥AC于点D,过点C作⊙O的切线,交OD的延长线于点E,连接AE.(1)求证:AE与⊙O相切;
(2)连接BD,若ED:DO=3:1,OA=9,求:
①AE的长;
②tanB的值.
考点:切线的判定与性质,勾股定理,相似三角形的判定与性质
专题:
分析:(1)连接OC,先证Rt△AOE≌Rt△COE,得出∠EAO=∠ECO,EC是⊙O的切线,所以∠EAO=90°,AE与⊙O相切;
(2)①根据ED:DO=3:1设出DO=t,则DE=3t,EO=4t,根据
=
,求得t=
,即EO=18,再用勾股定理即得AE的长;
②延长BD交AE于F,过O作OG∥AE交BD于G,得到△OGD∽△EFD.求得EF=3GO.因为O是AB的中点,所以AF=2GO,AE=5GO.求得GO、AF的长即可得tanB的值.
(2)①根据ED:DO=3:1设出DO=t,则DE=3t,EO=4t,根据
| AO |
| DO |
| EO |
| AO |
| 9 |
| 2 |
②延长BD交AE于F,过O作OG∥AE交BD于G,得到△OGD∽△EFD.求得EF=3GO.因为O是AB的中点,所以AF=2GO,AE=5GO.求得GO、AF的长即可得tanB的值.
解答:解:(1)连接OC,

∵OD⊥AC,OC=OA,
∴∠AOD=∠COD.
在△AOE和△COE中
∴Rt△AOE≌Rt△COE(SAS),
∴∠EAO=∠ECO.
又∵EC是⊙O的切线,
∴∠ECO=90°.
∴∠EAO=90°.
∴AE与⊙O相切;
(2)①设DO=t,则DE=3t,EO=4t,
∵
=
,即
=
,
∴t=
,即EO=18.
∴AE=
=
=9
;
②延长BD交AE于F,过O作OG∥AE交BD于G,

∵OG∥AE,
∴∠FED=∠GOD.
又∵∠EDF=∠ODG,
∴△OGD∽△EFD.
=
=
,即EF=3GO.
又∵O是AB的中点,
∴AF=2GO.
∴AE=AF+FE=5GO.
∴5GO=9
,
∴GO=
.
∴AF=
.
∴tanB=
=
.

∵OD⊥AC,OC=OA,
∴∠AOD=∠COD.
在△AOE和△COE中
|
∴Rt△AOE≌Rt△COE(SAS),
∴∠EAO=∠ECO.
又∵EC是⊙O的切线,
∴∠ECO=90°.
∴∠EAO=90°.
∴AE与⊙O相切;
(2)①设DO=t,则DE=3t,EO=4t,
∵
| AO |
| DO |
| EO |
| AO |
| 9 |
| t |
| 4t |
| 9 |
∴t=
| 9 |
| 2 |
∴AE=
| EO2-AO2 |
| 182-92 |
| 3 |
②延长BD交AE于F,过O作OG∥AE交BD于G,

∵OG∥AE,
∴∠FED=∠GOD.
又∵∠EDF=∠ODG,
∴△OGD∽△EFD.
| EF |
| OG |
| ED |
| DO |
| 3 |
| 1 |
又∵O是AB的中点,
∴AF=2GO.
∴AE=AF+FE=5GO.
∴5GO=9
| 3 |
∴GO=
9
| ||
| 5 |
∴AF=
18
| ||
| 5 |
∴tanB=
| AF |
| AB |
| ||
| 5 |
点评:本题主要考查了切线的判定与性质,勾股定理,相似三角形的判定与性质,综合性较强.

练习册系列答案
相关题目
分式方程
-1=
的解为( )
| 1 |
| x-2 |
| 1 |
| 2-x |
| A、x=4 | B、x=2 |
| C、x=0 | D、无解 |


 如图,已知抛物线C1与坐标轴的交点依次是A(-4,0),B(-2,0),E(0,8).
如图,已知抛物线C1与坐标轴的交点依次是A(-4,0),B(-2,0),E(0,8).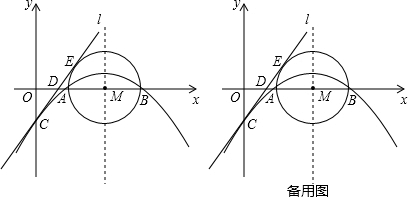
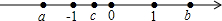 实数a、b、c,如图,化简
实数a、b、c,如图,化简