题目内容
14.(1)如图(1),△ABC中,点D、E分别在边AB、AC上,且$\frac{AD}{AB}$=$\frac{AE}{AC}$.求证:△ADE∽△ABC.(2)将矩形ABCD对角线平均分成12段,连接成图(2),若矩形ABCD内部空白部分面积总和是10cm2,则阴影部分面积总和是14cm2.
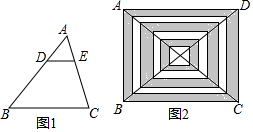
分析 (1)根据两边成比例夹角相等两三角形相似即可判断.
(2)设矩形ABCD的面积为S,由题意$\frac{1}{36}$S+($\frac{1}{4}$-$\frac{1}{9}$)S+($\frac{25}{36}$-$\frac{16}{36}$)S=10,解方程即可.
解答 (1)证明:∵$\frac{AD}{AB}$=$\frac{AE}{AC}$,∠A=∠A,
∴△ADE∽△ABC.
(2)解:设矩形ABCD的面积为S,
由题意$\frac{1}{36}$S+($\frac{1}{4}$-$\frac{1}{9}$)S+($\frac{25}{36}$-$\frac{16}{36}$)S=10,
解得S=24,
24-10=14,
∴阴影部分面积总和是14.
故答案为14.
点评 本题考查相似三角形的判定和性质、矩形的性质等知识,解题的关键是灵活运用所学知识,学会用方程思想思考问题,属于中考常考题型.

练习册系列答案
相关题目
4.下列调查中,适合普查的事件是( )
| A. | 调查华为手机的使用寿命 | |
| B. | 调查你班学生打网络游戏的情况 | |
| C. | 调查平顶山市七年级学生的心理健康情况 | |
| D. | 中央电视台财经频道《是真的吗》的节目收视率 |
5.甲、乙两同学从学校出发到县城去,甲每小时走4千米,乙每小时走6千米,甲先出发1小时,结果乙还比甲早到1小时,若设学校与县城间的距离为s千米,则以下方程正确的是( )
| A. | $\frac{s}{4}$+1=$\frac{s}{6}$-1 | B. | $\frac{s}{4}$=$\frac{s}{6}$-1 | C. | $\frac{s}{4}$-1=$\frac{s}{6}$+1 | D. | 4s-1=6s+1 |
9.若点P(1,a)与Q(b,2)关于x轴对称,则代数式(a+b)2017的值为( )
| A. | -1 | B. | 1 | C. | -2 | D. | 2 |
19.某机械厂七月份生产零件60万个,第三季度生产零件268万个,设该厂八、九月份平均每月的增长率为x,那么x满足的方程是( )
| A. | 60(1+x2)=268 | B. | 60+60(1+x2)=268 | ||
| C. | 60+60(1+x)+60(1+2x)=268 | D. | 60+60(1+x)+60(1+x2)=268 |
6.下列调查中,适宜采用普查方式的是( )
| A. | 考察人们保护环境的意识 | |
| B. | 了解全国九年级学生身高的现状 | |
| C. | 了解一批灯泡的寿命 | |
| D. | 检查一枚用于发射卫星的运载火箭的各零部件 |

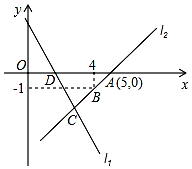 如图,直线l1的函数解析式为y=-2x+4,且l1与x轴交于点D,直线l2经过点A、B,直线l1、l2交于点C.
如图,直线l1的函数解析式为y=-2x+4,且l1与x轴交于点D,直线l2经过点A、B,直线l1、l2交于点C.