题目内容
11.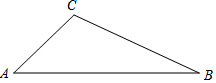 (1)用尺规作图,请作出△ABC的外接圆;
(1)用尺规作图,请作出△ABC的外接圆;(2)若∠ACB=120°,AB=6,求弓形ACB的面积.
分析 (1)先作出AC与BC的垂直平分线,交于点O,则点O为圆心,再作出△ABC的外接圆即可;
(2)连接AO,BO,过O作OD⊥AB于D,根据弓形ACB的面积=扇形OAB的面积-△AOB的面积,进行计算即可.
解答 解:(1)如图所示,⊙O即为所求;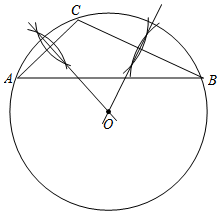
(2)如图所示,连接AO,BO,过O作OD⊥AB于D,
∵∠ACB=120°,AB=6,
∴∠AOB=120°,AD=$\frac{1}{2}$AB=3,
∴∠DAO=30°,
∴OD=$\sqrt{3}$,AO=2$\sqrt{3}$,
∴弓形ACB的面积=扇形OAB的面积-△AOB的面积
=$\frac{120×π×(2\sqrt{3})^{2}}{360}$-$\frac{1}{2}$×6×$\sqrt{3}$
=4π-3$\sqrt{3}$.
点评 本题主要考查了复杂作图,解题时需要运用垂径定理以及圆周角定理.找一个三角形的外心,就是找一个三角形的两条边的垂直平分线的交点,三角形的外接圆只有一个.

练习册系列答案
相关题目
16.某城市对用户的自来水收费实行阶梯水价,收费标准如表所示:
(1)某用户5月份缴水费45元,则该用户5月份的用水量是多少?
(2)若某用户的月用水量为m吨,请用含m的代数式表示该用户月所缴水费.
| 月用水量 | 不超过12吨的部分 | 超过12吨不超过18吨的部分 | 超过18吨的部分 |
| 收费标准(元/吨) | 2.00 | 2.50 | 3.00 |
(2)若某用户的月用水量为m吨,请用含m的代数式表示该用户月所缴水费.
1.到三角形三边距离相等的点是( )
| A. | 三条高的交点 | B. | 三条中线的交点 | ||
| C. | 三条角平分线的交点 | D. | 不能确定 |
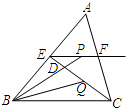 如图所示,在△ABC中,BC=4,E、F分别是AB、AC上的点,且EF∥BC,动点P在射线EF上,BP交CE于点D,∠CBP的平分线交CE于Q,当CQ=$\frac{1}{3}$CE时,EP+BP=8.
如图所示,在△ABC中,BC=4,E、F分别是AB、AC上的点,且EF∥BC,动点P在射线EF上,BP交CE于点D,∠CBP的平分线交CE于Q,当CQ=$\frac{1}{3}$CE时,EP+BP=8. 如图,△ABC中,AB=AC,∠A=36°,请你利用尺规在AC边上求一点P,使∠PBC=36°(不写作法,保留作图痕迹)
如图,△ABC中,AB=AC,∠A=36°,请你利用尺规在AC边上求一点P,使∠PBC=36°(不写作法,保留作图痕迹) 如图,平行四边形ABCD的周长为36,对角线AC,BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长是15.
如图,平行四边形ABCD的周长为36,对角线AC,BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长是15.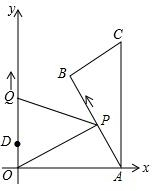 如图,Rt△ABC中,∠B=90°,∠CAB=30°,AC⊥x轴,它的顶点A的坐标为(10,0),C(10,$\frac{20\sqrt{3}}{3}$),点P从点A出发,沿A→B→C的方向匀速运动,同时点Q从点D(0,2)出发,沿y轴正方向以相同速度运动,当点P到达点C时,两点同时停止运动,若P点的速度为2单位/秒,设P运动的时间为t秒.
如图,Rt△ABC中,∠B=90°,∠CAB=30°,AC⊥x轴,它的顶点A的坐标为(10,0),C(10,$\frac{20\sqrt{3}}{3}$),点P从点A出发,沿A→B→C的方向匀速运动,同时点Q从点D(0,2)出发,沿y轴正方向以相同速度运动,当点P到达点C时,两点同时停止运动,若P点的速度为2单位/秒,设P运动的时间为t秒. 尺规作图:如图,BC是四边形ABCD的最大边,试以BC为一边用尺规作一个三角形,使它的面积等于四边形ABCD的面积.
尺规作图:如图,BC是四边形ABCD的最大边,试以BC为一边用尺规作一个三角形,使它的面积等于四边形ABCD的面积.