题目内容
6. 如图,平行四边形ABCD的周长为36,对角线AC,BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长是15.
如图,平行四边形ABCD的周长为36,对角线AC,BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长是15.
分析 根据平行四边形的对边相等和对角线互相平分可得,OB=OD,又因为E点是CD的中点,可得OE是△BCD的中位线,可得OE=$\frac{1}{2}$BC,所以易求△DOE的周长.
解答 解:∵?ABCD的周长为36,
∴2(BC+CD)=36,则BC+CD=18.
∵四边形ABCD是平行四边形,对角线AC,BD相交于点O,BD=12,
∴OD=OB=$\frac{1}{2}$BD=6.
又∵点E是CD的中点,
∴OE是△BCD的中位线,DE=$\frac{1}{2}$CD,
∴OE=$\frac{1}{2}$BC,
∴△DOE的周长=OD+OE+DE=$\frac{1}{2}$BD+$\frac{1}{2}$(BC+CD)=6+9=15,
即△DOE的周长为15.
故答案为:15.
点评 本题考查了三角形中位线定理、平行四边形的性质.解题时,利用了“平行四边形对角线互相平分”、“平行四边形的对边相等”的性质.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
1.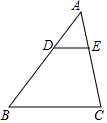 如图,在△ABC中,DE∥BC,若$\frac{AD}{DB}$=$\frac{2}{3}$,则$\frac{DE}{BC}$=( )
如图,在△ABC中,DE∥BC,若$\frac{AD}{DB}$=$\frac{2}{3}$,则$\frac{DE}{BC}$=( )
 如图,在△ABC中,DE∥BC,若$\frac{AD}{DB}$=$\frac{2}{3}$,则$\frac{DE}{BC}$=( )
如图,在△ABC中,DE∥BC,若$\frac{AD}{DB}$=$\frac{2}{3}$,则$\frac{DE}{BC}$=( )| A. | $\frac{2}{3}$ | B. | $\frac{1}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{5}$ |
18. 如图,两条公路OA和OB相交于O点,在∠AOB的内部有工厂C和D,现要修一个货站P,使得货站P到两公路OA、OB的距离相等,且到两工厂C、D的距离相等,用尺规作出货运站P的位置.(保留作图痕迹)
如图,两条公路OA和OB相交于O点,在∠AOB的内部有工厂C和D,现要修一个货站P,使得货站P到两公路OA、OB的距离相等,且到两工厂C、D的距离相等,用尺规作出货运站P的位置.(保留作图痕迹)
 如图,两条公路OA和OB相交于O点,在∠AOB的内部有工厂C和D,现要修一个货站P,使得货站P到两公路OA、OB的距离相等,且到两工厂C、D的距离相等,用尺规作出货运站P的位置.(保留作图痕迹)
如图,两条公路OA和OB相交于O点,在∠AOB的内部有工厂C和D,现要修一个货站P,使得货站P到两公路OA、OB的距离相等,且到两工厂C、D的距离相等,用尺规作出货运站P的位置.(保留作图痕迹)
16.点(2,5),(4,5)是抛物线y=ax2+bx+c上的两点,那么该抛物线的对称轴为( )
| A. | x=-$\frac{b}{a}$ | B. | x=1 | C. | x=0 | D. | x=3 |
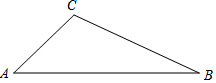 (1)用尺规作图,请作出△ABC的外接圆;
(1)用尺规作图,请作出△ABC的外接圆;