题目内容
10.通分:(1)$\frac{1}{a}$,$\frac{3}{4{a}^{2}b}$,$\frac{1}{6a{b}^{2}c}$;
(2)$\frac{2}{9-3a}$,$\frac{a-1}{{a}^{2}-9}$,$\frac{a}{{a}^{2}-6a+9}$.
分析 把几个异分母的分式分别化为与原来的分式相等的同分母的分式,依此确定最简公分母即可求解.
解答 解:(1)$\frac{1}{a}$=$\frac{12a{b}^{2}c}{12{a}^{2}{b}^{2}c}$,$\frac{3}{4{a}^{2}b}$=$\frac{9bc}{12{a}^{2}{b}^{2}c}$,$\frac{1}{6a{b}^{2}c}$$\frac{2a}{12{{a}^{2}b}^{2}c}$;
(2)$\frac{2}{9-3a}$=-$\frac{2}{3(a-3)}$=-$\frac{2(a+3)(a-3)}{3(a-3)^{2}(a+3)}$,$\frac{a-1}{{a}^{2}-9}$=$\frac{3(a-1)(a-3)}{3(a-3)^{2}(a+3)}$,$\frac{a}{{a}^{2}-6a+9}$=$\frac{a}{(a-3)^{2}}$=$\frac{3a(a+3)}{3(a-3)^{2}(a+3)}$.
点评 此题考查了通分,解答此题的关键是熟知找公分母的方法:
(1)系数取各系数的最小公倍数;
(2)凡出现的因式都要取;
(3)相同因式的次数取最高次幂.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
1.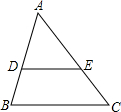 如图,在△ABC中,DE∥BC,AD=EC,DB=1,AE=4,则AC的长为( )
如图,在△ABC中,DE∥BC,AD=EC,DB=1,AE=4,则AC的长为( )
 如图,在△ABC中,DE∥BC,AD=EC,DB=1,AE=4,则AC的长为( )
如图,在△ABC中,DE∥BC,AD=EC,DB=1,AE=4,则AC的长为( )| A. | 5 | B. | 7 | C. | $\frac{12}{5}$ | D. | 6 |
15.小李上星期五买进某公司股票500股,每股60元,下表为本星期该股票的涨跌情况(单位:元).
(1)每周三收盘时,小李所持股票每股多少元?
(2)本星期内,股票最高价出现在星期几?是多少元?最低价出现在星期几?是多少元?
(3)已知买进股票时付了0.15%的手续费,卖出时需付成交额的0.15%的手续费和0.1%的交易费,若在本星期五收盘前将股票一次性卖出,他的收益如何?
| 星期 | 一 | 二 | 三 | 四 | 五 |
| 每股涨跌 | +2 | -0.5 | +1.5 | -1.8 | +0.8 |
(2)本星期内,股票最高价出现在星期几?是多少元?最低价出现在星期几?是多少元?
(3)已知买进股票时付了0.15%的手续费,卖出时需付成交额的0.15%的手续费和0.1%的交易费,若在本星期五收盘前将股票一次性卖出,他的收益如何?
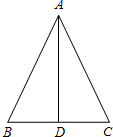 已知,△ANC中,AB=17cm,BC=16cm,BC边上的中线AD=15cm,求:
已知,△ANC中,AB=17cm,BC=16cm,BC边上的中线AD=15cm,求: