题目内容
20.若非零实数a,b满足4a2+b2=4ab,则$\frac{a}{b}$=$\frac{1}{2}$.分析 已知等式两边除以b2,利用完全平方公式变形,计算即可求出所求式子的值.
解答 解:已知等式4a2+b2=4ab两边除以b2,得:4($\frac{a}{b}$)2-4•$\frac{a}{b}$+1=0,即(2•$\frac{a}{b}$-1)2=0,
解得:$\frac{a}{b}$=$\frac{1}{2}$,
故答案为:$\frac{1}{2}$
点评 此题考查了因式分解-运用公式法,熟练掌握完全平方公式是解本题的关键.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
15.下列各组数中,运算结果为负数的是( )
| A. | 2-3 | B. | (-2)-3 | C. | 3-2 | D. | (-3)2 |
12.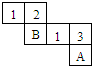 已知一个正方体的每一个表面都填有一个唯一的数字,且各相对的表面上所填的数互为倒数.若这个正方体的表面展开图如图所示,则A、B的值分别是( )
已知一个正方体的每一个表面都填有一个唯一的数字,且各相对的表面上所填的数互为倒数.若这个正方体的表面展开图如图所示,则A、B的值分别是( )
 已知一个正方体的每一个表面都填有一个唯一的数字,且各相对的表面上所填的数互为倒数.若这个正方体的表面展开图如图所示,则A、B的值分别是( )
已知一个正方体的每一个表面都填有一个唯一的数字,且各相对的表面上所填的数互为倒数.若这个正方体的表面展开图如图所示,则A、B的值分别是( )| A. | $\frac{1}{3}$,$\frac{1}{2}$ | B. | $\frac{1}{3}$,1 | C. | $\frac{1}{2}$,$\frac{1}{3}$ | D. | 1,$\frac{1}{3}$ |
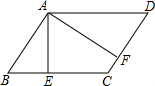 如图,已知:在?ABCD中,AE⊥BC于点E,AF⊥CD于点F,且∠EAF=60°,BE=2cm,DF=3cm,求?ABCD的周长和面积.
如图,已知:在?ABCD中,AE⊥BC于点E,AF⊥CD于点F,且∠EAF=60°,BE=2cm,DF=3cm,求?ABCD的周长和面积.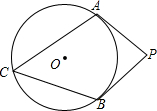 如图,PA、PB是⊙O的两条切线,点C在⊙O上,若∠APB=80°,则∠ACB=50度.
如图,PA、PB是⊙O的两条切线,点C在⊙O上,若∠APB=80°,则∠ACB=50度. 如图,已知线段AB
如图,已知线段AB