题目内容
11.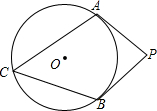 如图,PA、PB是⊙O的两条切线,点C在⊙O上,若∠APB=80°,则∠ACB=50度.
如图,PA、PB是⊙O的两条切线,点C在⊙O上,若∠APB=80°,则∠ACB=50度.
分析 连接OA、OB,由已知的PA、PB与圆O分别相切于点A、B,根据切线的性质得到OA⊥AP,OB⊥PB,从而得到∠OAP=∠OBP=90°,然后由已知的∠P的度数,根据四边形的内角和为360°,求出∠AOB的度数,最后根据同弧所对的圆周角等于它所对圆心角度数的一半即可得到∠ACB的度数.
解答 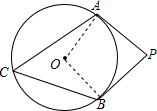 解:连接OA、OB,
解:连接OA、OB,
∵PA、PB与圆O分别相切于点A、B,
∴OA⊥AP,OB⊥PB,
∴∠OAP=∠OBP=90°,又∠APB=80°,
∴∠AOB=360°-90°-90°-80°=100°,
又∵∠ACB和∠AOB分别是$\widehat{AB}$所对的圆周角和圆心角,
∴∠ACB=$\frac{1}{2}$∠AOB=$\frac{1}{2}$×100°=50°
点评 此题考查了切线的性质,以及圆周角定理.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题,同时要求学生掌握同弧所对的圆周角等于所对圆心角的一半.

练习册系列答案
相关题目
1.点(4,-5)关于y轴的对称点的坐标是( )
| A. | (4,5) | B. | (-4,-5) | C. | (-4,5) | D. | (-5,4) |
6.下列四个几何体中,左视图与其它三个不同的是( )
| A. |  | B. |  | C. |  | D. |  |

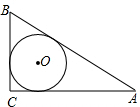 如图,Rt△ABC中,∠C=90°,若AC=4,BC=3,则△ABC的内切圆半径r=1.
如图,Rt△ABC中,∠C=90°,若AC=4,BC=3,则△ABC的内切圆半径r=1.