题目内容
9. 如图,在△ABC中,∠B>∠C,AD⊥BC,垂足为D,AE平分∠BAC.
如图,在△ABC中,∠B>∠C,AD⊥BC,垂足为D,AE平分∠BAC. (1)已知∠B=60°,∠C=30°,求∠DAE的度数;
(2)已知∠B=3∠C,说明:∠DAE=∠C.
分析 (1)首先利用三角形内角和定理求得∠BAC的度数,则∠BAE即可求得,然后在直角△ABD中求得∠BAD的度数,根据∠DAE=∠BAE-∠BAD求解;
(2)设∠C=x,则∠B=3x,利用(1)的思路表示出∠DAE即可证得.
解答 解:(1)∵∠BAC=180°-∠B-∠C=180°-60°-30°=90°,
又∵AE平分∠BAC,
∴∠BAE=$\frac{1}{2}$∠BAC=45°.
∵直角△ABD中,∠BAD=90°-∠B=90°-60°=30°,
∴∠DAE=∠BAE-∠BAD=45°-30°=15°;
(2)设∠C=x,则∠B=3x∴∠BAC=180°-4x
∵AE平分∠BAC,
∴∠BAE=90-2x,
∵AD⊥BC,
∴∠BAD=90-3x,
∴∠DAE=∠BAE-∠BAD=(90-2x)-(90-3x)=x,
∴∠DAE=∠C.
点评 本题考查了三角形的内角和定理和定理,正确利用x表示出∠DAE的度数是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.如图,把一个矩形的纸片按图示对折两次,然后剪下一部分,为了得到一个钝角为110°的菱形,剪口与第二次折痕所成角的度数应为( )
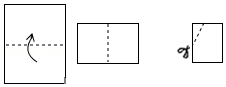

| A. | 70°或20° | B. | 55°或45° | C. | 55°或35° | D. | 55°或65° |
4.若|a|<2,且a是整数,那么a为( )
| A. | 2,1,0 | B. | -2,-1,0,1,2 | C. | -1,0,1 | D. | 0,-1,-2 |
 如图,在△ABC中,AB=AC.
如图,在△ABC中,AB=AC. 如图,P是菱形ABCD对角线BD上一点,PE⊥AB于点E,PE=4cm,则点P到BC的距离是4cm.
如图,P是菱形ABCD对角线BD上一点,PE⊥AB于点E,PE=4cm,则点P到BC的距离是4cm.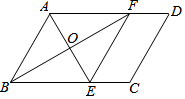 如图,在?ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,AE与BF相交于点O,连接EF.
如图,在?ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,AE与BF相交于点O,连接EF. 如图,A、B两点被池塘隔开,在AB外选一点C,连接AC、BC,取AC、BC的中点D、E,量出DE=a,则AB=2a,它的根据是三角形的中位线等于第三边的一半.
如图,A、B两点被池塘隔开,在AB外选一点C,连接AC、BC,取AC、BC的中点D、E,量出DE=a,则AB=2a,它的根据是三角形的中位线等于第三边的一半. 如图,已知AD=AE,∠BEC=∠CDB,BD、CE相交于点O.
如图,已知AD=AE,∠BEC=∠CDB,BD、CE相交于点O.