题目内容
 如图,AC=AE,AB=AD,∠1=∠2.
如图,AC=AE,AB=AD,∠1=∠2.(1)求证:∠B=∠D;
(2)若△ADE绕A点逆时针旋转,使∠1=90°时,直线BC、DE的关系如何?给出证明,当∠BAD为平角时呢?
考点:全等三角形的判定与性质
专题:
分析:(1)由条件可证明△ABC≌△EAD,可得出结论;
(2)画出相应的图形可以证明出结论,当∠1=90°时,可证明BC=DE且BC⊥DE,当∠BAD为平角时,BC和DE平行.
(2)画出相应的图形可以证明出结论,当∠1=90°时,可证明BC=DE且BC⊥DE,当∠BAD为平角时,BC和DE平行.
解答:(1)证明:
∵∠1=∠2,
∴∠1+∠CAD=∠2+∠CAD,
即∠EAD=∠CAB,
在△ABC和△ADE中
∴△ABC≌△EAD(SAS),
∴∠B=∠D;
(2)解:
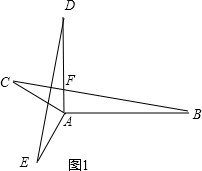
当∠1=90°时,如图1,
设AD和BC交于点F,
∵∠1=90°,
∴∠B+∠AFB=90°,
且由(1)知∠B=∠D,
∴∠D+∠DFC=90°,
即DE⊥BC,且DE=BC,
当∠DAB=180°时,如图2,
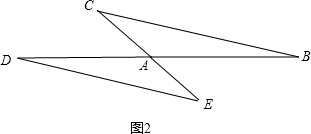
由全等可知∠B=∠D,
所以BC∥DE,且BC=DE.
∵∠1=∠2,
∴∠1+∠CAD=∠2+∠CAD,
即∠EAD=∠CAB,
在△ABC和△ADE中
|
∴△ABC≌△EAD(SAS),
∴∠B=∠D;
(2)解:

当∠1=90°时,如图1,
设AD和BC交于点F,
∵∠1=90°,
∴∠B+∠AFB=90°,
且由(1)知∠B=∠D,
∴∠D+∠DFC=90°,
即DE⊥BC,且DE=BC,
当∠DAB=180°时,如图2,

由全等可知∠B=∠D,
所以BC∥DE,且BC=DE.
点评:本题主要考查全等三角形的判定和性质,掌握全等三角形的判定方法是解题的关键.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
 已知:如图,抛物线y=ax2+bx+c(a≠0)经过X轴上的两点A(x1,0)、B(x2,0)和y轴上的点C(0,-1.5),⊙P的圆心P在y轴上,且经过B、C两点,若b=
已知:如图,抛物线y=ax2+bx+c(a≠0)经过X轴上的两点A(x1,0)、B(x2,0)和y轴上的点C(0,-1.5),⊙P的圆心P在y轴上,且经过B、C两点,若b= 如图,长方形ABCD被分成6个小长方形,其中4个的面积已标在图中,试求未知的两个长方形的面积.
如图,长方形ABCD被分成6个小长方形,其中4个的面积已标在图中,试求未知的两个长方形的面积. 如图,在四边形ABCD中,∠B=∠D=90°,∠A=150°,AB=5,CD=15,求AD、BC的长.
如图,在四边形ABCD中,∠B=∠D=90°,∠A=150°,AB=5,CD=15,求AD、BC的长.