题目内容
10.若$\frac{1}{2}$|2x-1|+$\frac{1}{3}$|y-4|=0,则多项式1-xy-x2y的值为-$\frac{5}{4}$.分析 利用非负数的性质,当几个数或式的绝对值相加和为0时,则其中的每一项都必须等于0.
解答 解:∵$\frac{1}{2}$|2x-1|+$\frac{1}{3}$|y-4|=0,
∴2x-1=0,y-4=0,
解得:x=$\frac{1}{2}$,y=4,
∴1-$\frac{1}{2}$×4-${(\frac{1}{2})}^{2}$×4=1-2-$\frac{1}{4}$=$-\frac{5}{4}$,
故答案为:$-\frac{5}{4}$.
点评 本题主要考查了非负数的性质,当几个数或式的绝对值相加和为0时,则其中的每一项都必须等于0是解答此题的关键.

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
20.已知两点A(5,6)、B(7,2),先将线段AB向左平移一个单位,再以原点O为位似中心,在第一象限内将其缩小为原来的$\frac{1}{2}$得到线段CD,则点A的对应点C的坐标为( )
| A. | (2,3) | B. | (3,1) | C. | (2,1) | D. | (3,3) |
18.在$\frac{1}{4}$,-1,0,2这四个数中,属于负数的是( )
| A. | $\frac{1}{4}$ | B. | -1 | C. | 0 | D. | 2 |
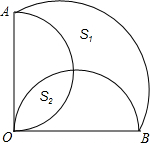 如图,扇形OAB的圆心角是90°,分别以OA、OB为直径在扇形内作圆,则S1、S2两部分图形面积的大小关系是什么?
如图,扇形OAB的圆心角是90°,分别以OA、OB为直径在扇形内作圆,则S1、S2两部分图形面积的大小关系是什么?