题目内容
5.二次函数y=ax2+bx+c,过点(-2,0)且顶点为(1,3),则其对称轴为x=1,开口向下,与x轴另一交点为(4,0),x=1时,y的最值为3.分析 由抛物线的顶点坐标可知抛物线的对称轴为x=1,y的最值为3,然后根据根据抛物线的对称性可求得与x轴另一交点为(4,0),根据点(-2,0)且顶点为(1,3)的位置关系可知抛物线的开口方向.
解答 解:∵抛物线的顶点坐标为(1,3),
∴抛物线的对称轴为x=1,当x=1时,y的最值为3.
∵抛物线的对称轴为x=1,
∴点(-2,0)关于x=1的对称点为(4,0).
∴抛物线与x轴另一交点为(4,0).
根据(-2,0)、(1,3)、(4,0)三点的坐标画出抛物线的大致图象可知,抛物线的开口向下.
故答案为:x=1;向下;(4,0);1;3.
点评 本题主要考查的是二次函数的性质,掌握二次函数的图象和性质是解题的关键.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
20.某次歌唱比赛,最后三名选手的成绩统计如表:
(1)若按算术平均分排出冠军、亚军、季军,则冠军、亚军、季军各是谁?
(2)若按6:3:1的加权平均分排出冠军、亚军、季军,则冠军、亚军、季军各是谁?
(3)若最后排名冠军是王晓丽,亚军是李真,季军是林飞扬,则权重可能是多少?
| 比赛项目 | 比赛成绩/分 | ||
| 王晓丽 | 李真 | 林飞扬 | |
| 唱功 | 98 | 95 | 80 |
| 音乐常识 | 80 | 90 | 100 |
| 综合知识 | 80 | 90 | 100 |
(2)若按6:3:1的加权平均分排出冠军、亚军、季军,则冠军、亚军、季军各是谁?
(3)若最后排名冠军是王晓丽,亚军是李真,季军是林飞扬,则权重可能是多少?
14.直线y=2x+2沿y轴向下平移6个单位后与x轴的交点坐标是( )
| A. | (-4,0) | B. | (-1,0) | C. | (0,2) | D. | (2,0) |
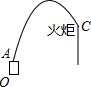 如图是某运动会开幕式点燃火炬的示意图,发射台OA的高度为2m,火炬的高度为12m,距发射台OA的水平距离为20m,在A处的发射装置向目标C发射一个火球点燃火炬,该火球运动的轨迹为抛物线形,当火球运动到距离地面最大高度20m时,相应的水平距离为12m,请你判断该火球能否点燃目标C?并说明理由.
如图是某运动会开幕式点燃火炬的示意图,发射台OA的高度为2m,火炬的高度为12m,距发射台OA的水平距离为20m,在A处的发射装置向目标C发射一个火球点燃火炬,该火球运动的轨迹为抛物线形,当火球运动到距离地面最大高度20m时,相应的水平距离为12m,请你判断该火球能否点燃目标C?并说明理由.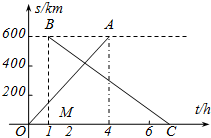 甲、乙两城市之间开通了动车组高速列车.已知每隔2h有一列速度相同的动车组列车从甲城开往乙城.如图,OA是第一列动车组列车离开甲城的路程s(km)与运行时间t(h)的函数图象,BC是一列从乙城开往甲城的普通快车距甲城的路程s(km)与运行时间t(h)的函数图象.请根据图中的信息,解答下列问题:
甲、乙两城市之间开通了动车组高速列车.已知每隔2h有一列速度相同的动车组列车从甲城开往乙城.如图,OA是第一列动车组列车离开甲城的路程s(km)与运行时间t(h)的函数图象,BC是一列从乙城开往甲城的普通快车距甲城的路程s(km)与运行时间t(h)的函数图象.请根据图中的信息,解答下列问题: