题目内容
18．
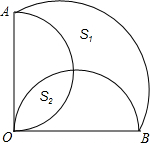如图，扇形OAB的圆心角是90°，分别以OA、OB为直径在扇形内作圆，则S1、S2两部分图形面积的大小关系是什么？
分析 假设出扇形半径，再表示出半圆面积，以及扇形面积，进而即可表示出S1、S2的面积的关系．
解答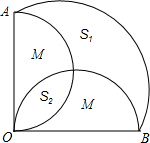 
解：∵扇形OAB的圆心角为90°，假设扇形半径为a，
∴扇形面积为：$\frac{90π×{a}^{2}}{360}$=$\frac{{πa}^{2}}{4}$，
半圆面积为：$\frac{1}{2}$×π×（$\frac{a}{2}$）2=$\frac{{πa}^{2}}{8}$，
∴S1+SM =SM+S2=$\frac{{πa}^{2}}{8}$，
∴S1=S2，即S1、S2两部分图形面积的大小相等．
点评 此题主要考查了扇形面积求法，根据已知得出半圆面积以及扇形面积是解题关键．
练习册系列答案
相关题目
7．-6的绝对值等于（ ）
| A． | -6 | B． | 6 | C． | -$\frac{1}{6}$ | D． | $\frac{1}{6}$ |
6．式子$\sqrt{2x-1}$在实数范围内有意义，则x的取值范围是（ ）
| A． | x＜$\frac{1}{2}$ | B． | x≥0 | C． | x＞$\frac{1}{2}$ | D． | x≥$\frac{1}{2}$ |