题目内容
1．解方程：kx2+2（k-2）x+k-3=0．分析 分类讨论：当k=0方程为一元一次方程，易得x=-$\frac{3}{4}$；当k≠0，先计算判别式的值，然后根据判别式的意义，利用求根公式求解．
解答 解：当k=0时，方程变形为-4x-3=0，解得x=-$\frac{3}{4}$；
当k≠0，△=4（k-2）2-4k（k-3）=16-4k，
当k=4时，x1=x2=$\frac{-2（k-2）}{2k}$=-$\frac{1}{2}$，
当k＜4且k≠0时，x=$\frac{-2（k-2）±\sqrt{16-4k}}{2k}$，则x1=$\frac{2-k+\sqrt{4-k}}{k}$，x2=$\frac{2-k-\sqrt{4-k}}{k}$，
当k＞4时，方程没有实数解．
点评 本题考查了解一元二次方程-公式法：用求根公式解一元二次方程的方法是公式法．也考查了解一元一次方程．注意分类讨论．
练习册系列答案
相关题目
11．为鼓励人们节约用水，某地实行阶梯式计量水价（如下表所示）．
（1）若张红家5月份用水量为15吨，则该月需缴交水费24元；
（2）若张红家6月份缴交水费44元，则该月用水量为25吨；
（3）若张红家7月份用水量为a吨（a＞30），请计算该月需缴交水费多少元？（用含a的代数式表示）
| 级别 | 月用水量 | 水价 |
| 第1级 | 20吨以下（含20吨） | 1.6元/吨 |
| 第2级 | 20吨-30吨（含30吨） | 超过20吨部分按2.4元/吨 |
| 第3级 | 30吨以上 | 超过30吨部分按4.8元/吨 |
（2）若张红家6月份缴交水费44元，则该月用水量为25吨；
（3）若张红家7月份用水量为a吨（a＞30），请计算该月需缴交水费多少元？（用含a的代数式表示）
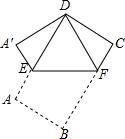请将矩形纸片ABCD如图所示折叠，使顶点B与顶点D重合，折痕为EF，若AB=$\sqrt{3}$，AD=3，则△DEF的周长为6．