题目内容
19. 在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E,F.
在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E,F.(1)若BE=CF,求证:AD是△ABC的角平分线.
(2)若AD是△ABC的角平分线,求证:BE=CF.
分析 (1)首先可证明Rt△BDE≌Rt△DCF(HL),再根据三角形角平分线的逆定理求得AD是△ABC的角平分线即可;
(2)根据角平分线上的点到角的两边的距离相等可得DE=DF,再利用“HL”证明Rt△BDE和Rt△CDF全等,然后根据全等三角形对应边相等即可证明.
解答 证明:(1)∵DE⊥AB,DF⊥AC,
∴△BDE△DCF是直角三角形.
在Rt△BDE与Rt△DCF中,
$\left\{\begin{array}{l}{BD=DC}\\{BE=CF}\end{array}\right.$,
∴Rt△BDE≌Rt△DCF(HL),
∴DE=DF,
又∵DE⊥AB,DF⊥AC,
∴AD是△ABC的角平分线;
(2)∵AD是△ABC的角平分线,DE⊥AB于E,DF⊥AC于F,
∴DE=DF,
∵AD是BC边的中线,
∴BD=CD,
在Rt△BDE和Rt△CDF中,
$\left\{\begin{array}{l}{BD=DC}\\{BE=CF}\end{array}\right.$,
∴Rt△BDE≌Rt△CDF(HL),
∴BE=CF.
点评 此题主要考查了角平分线的性质与判定,直角三角形全等的判定.要证边相等,想办法证明边所在的三角形全等,是常用的方法之一,要熟练掌握并灵活运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
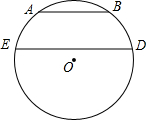 如图:AB、DE是⊙O的两条弦,且AB∥ED,求证:$\widehat{AD}$=$\widehat{BE}$.
如图:AB、DE是⊙O的两条弦,且AB∥ED,求证:$\widehat{AD}$=$\widehat{BE}$.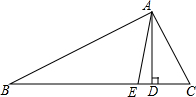 如图,三角形ABC中,∠C>∠B,AD是BC边上的高,AE是三角形中∠A的平分线.
如图,三角形ABC中,∠C>∠B,AD是BC边上的高,AE是三角形中∠A的平分线.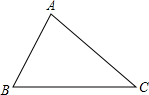 如图,利用尺规在平面内确定一点O,使得点O到△ABC的两边AB、AC的距离相等,并且点O到B、C两点的距离也相等(保留作图痕迹,不写作法).
如图,利用尺规在平面内确定一点O,使得点O到△ABC的两边AB、AC的距离相等,并且点O到B、C两点的距离也相等(保留作图痕迹,不写作法).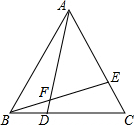 如图,D、E分别为等边△ABC的边BC、AC上的点,且BD=CE,连结BE、AD交于F,求证:∠AFE=60°.
如图,D、E分别为等边△ABC的边BC、AC上的点,且BD=CE,连结BE、AD交于F,求证:∠AFE=60°.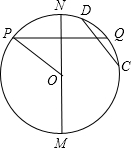 由垂径定理可知:垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧;平分弧的直径垂直平分这条弧所对的弦.请利用这一结论解决问题:
由垂径定理可知:垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧;平分弧的直径垂直平分这条弧所对的弦.请利用这一结论解决问题: