题目内容
某化工产品C是由A,B两种原料加工而成的,每个C产品的质量为50kg,经测定加工费与A的质量的平方成正比例;A原料的成本10元/kg,B原料的成本:40元/kg;C产品中A的含量不能低于10%,又不能高于60%;
(1)设每个C产品的成本为y(元),每个C产品含A的质量为x(kg),当一个C产品含A种原料10%时,成本价是1875元,求y与x之间的函数关系式,并写出x的范围;(每个C成本=A的成本+B的成本+加工费用)
(2)C产品出厂价经核算是所含B的质量的一次函数,且满足如下数表:
①求C产品的出厂价z(元)与含A的质量x(kg)之间的函数关系式;
②求每个C产品的利润w(元)与含A的质量x(kg)之间的函数关系式;(利润=出厂价-成本)
(3)若生产的产品都能销售出去,工厂生产哪一种含量的C产品获利最高,最高为多少;
(4)某客户买了100个相同的C产品,厂家获利50000元,问这种C产品中含A原料的百分比是多少.
(1)设每个C产品的成本为y(元),每个C产品含A的质量为x(kg),当一个C产品含A种原料10%时,成本价是1875元,求y与x之间的函数关系式,并写出x的范围;(每个C成本=A的成本+B的成本+加工费用)
(2)C产品出厂价经核算是所含B的质量的一次函数,且满足如下数表:
| 含A:x(kg) | 5 | 15 |
| 出厂价(元/50kg) | 2450 | 2350 |
②求每个C产品的利润w(元)与含A的质量x(kg)之间的函数关系式;(利润=出厂价-成本)
(3)若生产的产品都能销售出去,工厂生产哪一种含量的C产品获利最高,最高为多少;
(4)某客户买了100个相同的C产品,厂家获利50000元,问这种C产品中含A原料的百分比是多少.
考点:二次函数的应用
专题:
分析:(1)设y=10x+40(50-x)+ax2,利用当一个C产品含A种原料10%时,成本价是1875元,进而求出即可;
(2)利用待定系数法求一次函数解析式,进而得出w与x的函数解析式;
(3)利用配方法求出二次函数最值即可;
(4)根据题意得出
=-x2+20x+500,进而求出即可.
(2)利用待定系数法求一次函数解析式,进而得出w与x的函数解析式;
(3)利用配方法求出二次函数最值即可;
(4)根据题意得出
| 50000 |
| 100 |
解答:解:(1)设y=10x+40(50-x)+ax2,
由题意可知:x=50×10%=5时,y=1875,
∴1875=10×5+40(50-5)+a×52,
解得:a=1,
∴y=x2-30x+2000(5≤x≤30);
(2)①设z=k(50-x)+b(k、b为常数,k≠0),由题意得:
,
解得
,
∴z=-10x+2500;
②∴w=(-10x+2500)-(x2-30x+2000),
w=-x2+20x+500;
(3)由(2)知:w=-x2+20x+500,
∴w=-(x-10)2+600,
∴x=10,即生产含A:20%的C产品时,利润最高:最高利润为600元;
(4)由(2)知w=-x2+20x+500,
∴
=-x2+20x+500,
解得:x=0(舍)或x=20,
∴这种C产品中含A原料的百分比是40%.
由题意可知:x=50×10%=5时,y=1875,
∴1875=10×5+40(50-5)+a×52,
解得:a=1,
∴y=x2-30x+2000(5≤x≤30);
(2)①设z=k(50-x)+b(k、b为常数,k≠0),由题意得:
|
解得
|
∴z=-10x+2500;
②∴w=(-10x+2500)-(x2-30x+2000),
w=-x2+20x+500;
(3)由(2)知:w=-x2+20x+500,
∴w=-(x-10)2+600,
∴x=10,即生产含A:20%的C产品时,利润最高:最高利润为600元;
(4)由(2)知w=-x2+20x+500,
∴
| 50000 |
| 100 |
解得:x=0(舍)或x=20,
∴这种C产品中含A原料的百分比是40%.
点评:此题主要考查了二次函数的应用以及配方法求二次函数最值以及待定系数法求一次函数解析式等知识,正确得出函数解析式是解题关键.

练习册系列答案
相关题目
下列各数中,最大的数是( )
| A、-1 | ||
| B、2 | ||
| C、0 | ||
D、
|
 如图,抛物线的顶点为A(2,1),且经过原点O,与x轴的另一个交点为B.
如图,抛物线的顶点为A(2,1),且经过原点O,与x轴的另一个交点为B.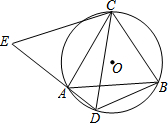 如图,△ABC是⊙O的内接三角形,AC=BC,点D是⊙O中弧AB的上的一点,延长DA至点E,使CE=CD.
如图,△ABC是⊙O的内接三角形,AC=BC,点D是⊙O中弧AB的上的一点,延长DA至点E,使CE=CD. 如图,在△ABC中,AB=AC,AD⊥BC,AE∥BC.
如图,在△ABC中,AB=AC,AD⊥BC,AE∥BC.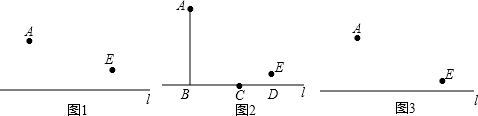
 在一次募捐活动中,某单位50名职工积极响应,同时将所捐款情况统计并制成统计图,根据图提供的信息,捐款金额的众数和中位数分别是
在一次募捐活动中,某单位50名职工积极响应,同时将所捐款情况统计并制成统计图,根据图提供的信息,捐款金额的众数和中位数分别是 如图,P是反比例函数y=
如图,P是反比例函数y=