题目内容
6.阅读下列解方程的过程,并完成(1)、(2)小题的解答.解方程:|x-1|=2
解:当x-1<0,即x<1时,原方程可化为:-(x-1)=2,解得x=-1;当x-1≥0,即x≥1时,原方程可化为:x-1=2,解得x=3;
综上所述,方程|x-1|=2的解为x=-1或x=3.
(1)解方程:|2x+3|=8.
(2)解方程:|2x+3|-|x-1|=1.
分析 (1)根据绝对值的性质,可化简方程,根据解一元一次方程,可得答案;
(2)根据绝对值的性质,可化简方程,根据解一元一次方程,可得答案.
解答 解:(1)当x<-$\frac{3}{2}$时,原方程等价于2x+3=-8,解得x=-$\frac{11}{2}$;
当x≥-$\frac{3}{2}$时,原方程等价于2x+3=8,解得x=$\frac{5}{2}$;
综上所述,方程|2x+3|=8的解为x=-$\frac{11}{2}$或x=$\frac{5}{2}$.
(2)当x<-$\frac{3}{2}$时,原方程等价于-x-4=1,解得x=-5;
当-$\frac{3}{2}$≤x<1时,原方程等价于3x+2=1,解得x=-$\frac{1}{3}$;
当x≥1时,原方程等价于x+4=1,解得x=-3,(不符合题意,舍);
综上所述,方程:|2x+3|-|x-1|=1的解为x=-5或x=-$\frac{1}{3}$.
点评 本题考查了含绝对值符号的一元一次方程,利用绝对值的性质化简方程是解题关键,要分类讨论,以防遗漏.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
1.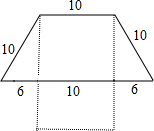 墙上钉着用一根彩绳围成的梯形形状的饰物,如图实线所示(单位:cm).小颖将梯形下底的钉子去掉,并将这条彩绳钉成一个长方形,如图虚线所示.小颖所钉长方形的长、宽各为多少厘米?如果设长方形的长为xcm,根据题意,可得方程为( )
墙上钉着用一根彩绳围成的梯形形状的饰物,如图实线所示(单位:cm).小颖将梯形下底的钉子去掉,并将这条彩绳钉成一个长方形,如图虚线所示.小颖所钉长方形的长、宽各为多少厘米?如果设长方形的长为xcm,根据题意,可得方程为( )
 墙上钉着用一根彩绳围成的梯形形状的饰物,如图实线所示(单位:cm).小颖将梯形下底的钉子去掉,并将这条彩绳钉成一个长方形,如图虚线所示.小颖所钉长方形的长、宽各为多少厘米?如果设长方形的长为xcm,根据题意,可得方程为( )
墙上钉着用一根彩绳围成的梯形形状的饰物,如图实线所示(单位:cm).小颖将梯形下底的钉子去掉,并将这条彩绳钉成一个长方形,如图虚线所示.小颖所钉长方形的长、宽各为多少厘米?如果设长方形的长为xcm,根据题意,可得方程为( )| A. | 2(x+10)=10×4+6×2 | B. | 2(x+10)=10×3+6×2 | C. | 2x+10=10×4+6×2 | D. | 2(x+10)=10×2+6×2 |
18.在某市开展的“好书伴我成长”读书活动中,某中学为了解八年级300名学生的读书情况,随机调查了八年级50名学生读书的册数,统计数据如表所示:
①求这50名学生读书册数的平均数,众数和中位数;
②估计该校八年级在本次活动中读书多于2册的学生人数占全年级的百分比.
| 册数 | 0 | 1 | 2 | 3 | 4 |
| 人数 | 3 | 13 | 16 | 17 | 1 |
②估计该校八年级在本次活动中读书多于2册的学生人数占全年级的百分比.
 如图所示,a⊥b,b∥c,∠1=120°,则∠2的度数是30°.
如图所示,a⊥b,b∥c,∠1=120°,则∠2的度数是30°. (1)计算:34°25′×3+35°42′
(1)计算:34°25′×3+35°42′