��Ŀ����
19����ƽ��ֱ������ϵ�У�OΪԭ�㣬��B��x����������ϣ�D��0��8����������OBCD�۵���ʹ�ö���B����CD���ϵ�P�㴦����I����ͼ�٣���֪�ۺ����BC���ڵ�A����OD=2CP�����A�����꣮
������ͼ���еĵ� P ǡ����CD�ߵ��е㣬���AOB�Ķ�����
������ͼ�ڣ��ڣ�I���������£���ȥ�ۺ�AO���߶�AP������BP������M���߶�OP�ϣ���M��P��O���غϣ�������N���߶�OB���ӳ����ϣ���BN=PM������MN��PB�ڵ�F����ME��BP�ڵ�E�����ʵ���M��N���ƶ������У��߶�EF�ij����Ƿ����仯�����仯��˵�����ɣ������䣬����߶�EF�ij��ȣ�ֱ��д��������ɣ�
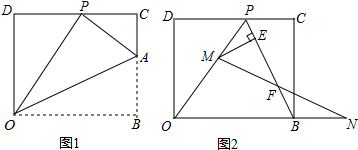
���� ��1����OB=OP=DC=x����DP=x-4����Rt��ODP�У�����OD2+DP2=OP2����ã�x=10��Ȼ����ݡ�ODP�ס�PCA�õ�AC=$\frac{x-4}{2}$=3���Ӷ��õ�AB=5����ʾ����A��10��5����
��2�����ݵ�Pǡ����CD�ߵ��е���DP=PC=y����DC=OB=OP=2y����Rt��ODP�У�����OD2+DP2=OP2����ã�y=$\frac{8\sqrt{3}}{3}$��Ȼ�����á�ODP�ס�PCA�õ�AC=$\frac{{y}^{2}}{8}$=$\frac{8}{3}$���Ӷ�����tan��AOB=$\frac{\sqrt{3}}{3}$�õ���AOB=30�㣻
��3����MQ��AN����PB�ڵ�Q�����MP=MQ��BN=QM���ó�MP=MQ������ME��PQ���ó�EQ=$\frac{1}{2}$PQ�����ݡ�QMF=��BNF��֤����MFQ�ա�NFB���ó�QF=$\frac{1}{2}$QB�������EF=$\frac{1}{2}$PB���ɣ�1���еĽ������PB��������EF=$\frac{1}{2}$PB���ɵó��߶�EF�ij��Ȳ��䣮
��� �⣺��1����D��0��8����
��OD=BC=8��
��OD=2CP��
��CP=4��
��OB=OP=DC=x��
��DP=x-4��
��Rt��ODP��OD2+DP2=OP2��
����82+��x-4��2=x2��
��ã�x=10��
�ߡ�OPA=��B=90�㣬
���ODP�ס�PCA��
��OD��PC=DP��CA��
��8��4=��x-4����AC��
��AC=$\frac{x-4}{2}$=3��
��AB=5��
���A��10��5����
��2���ߵ� P ǡ����CD�ߵ��е㣬
��DP=PC=y��
��DC=OB=OP=2y��
��Rt��ODP��OD2+DP2=OP2��
����82+y2=��2y��2��
��ã�y=$\frac{8\sqrt{3}}{3}$��
�ߡ�OPA=��B=90�㣬
���ODP�ס�PCA��
��OD��PC=DP��CA��
��8��y=y��AC��
��AC=$\frac{{y}^{2}}{8}$=$\frac{8}{3}$��
��AB=8-$\frac{8}{3}$=$\frac{16}{3}$��
��OB=2y=$\frac{16\sqrt{3}}{3}$��
��tan��AOB=$\frac{AB}{OB}$=$\frac{\frac{16}{3}}{\frac{16\sqrt{3}}{3}}$=$\frac{\sqrt{3}}{3}$��
���AOB=30�㣻 ��3����MQ��AN����PB�ڵ�Q����ͼ2��
��3����MQ��AN����PB�ڵ�Q����ͼ2��
��AP=AB��MQ��AN
���APB=��ABP=��MQP��
��MP=MQ��
��BN=PM��
��BN=QM��
��MP=MQ��ME��PQ��
��EQ=$\frac{1}{2}$PQ��
��MQ��AN��
���QMF=��BNF��
�ڡ�MFQ�͡�NFB�У�
$\left\{\begin{array}{l}{��QMF=��NFB}\\{��QMF=��BNF}\\{MQ=BN}\end{array}\right.$��
���MFQ�ա�NFB��AAS����
��QF=$\frac{1}{2}$QB��
��EF=EQ+QF=$\frac{1}{2}$PQ+$\frac{1}{2}$QB=$\frac{1}{2}$PB��
�ɣ����еĽ��ۿɵã�PC=4��BC=8����C=90�㣬
��PB=$\sqrt{{8}^{2}+{4}^{2}}$=4$\sqrt{5}$��
��EF=$\frac{1}{2}$PB=2$\sqrt{5}$��
���ڣ�1���������£�����M��N���ƶ������У��߶�EF�ij��Ȳ��䣬���ij���Ϊ2$\sqrt{5}$��
���� ���⿼�����������ۺϣ��õ���֪ʶ�������������ε��ж������ʡ�ȫ�������ε��ж������ʡ����ɶ��������������ε����ʣ��ؼ������������ߣ��ҳ�ȫ�Ⱥ����Ƶ������Σ�

 ��һ������ĩ�ٷֳ�̾�ϵ�д�
��һ������ĩ�ٷֳ�̾�ϵ�д�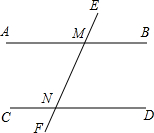 ��ͼ��ֱ��AB��CD��EF�ֱ�AB��CD�ڵ�M��N������AME=125�㣬���CNF�Ķ���Ϊ��������
��ͼ��ֱ��AB��CD��EF�ֱ�AB��CD�ڵ�M��N������AME=125�㣬���CNF�Ķ���Ϊ��������| A�� | 125�� | B�� | 75�� | C�� | 65�� | D�� | 55�� |
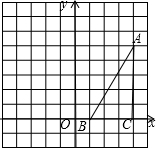 ��ͼ���ڷ���ֽ�У�С�����εı߳�Ϊ1������ABC�����������Ϊ��㣬����ABC��x������ƽ��5����λ���ȣ�����������ֱ������ϵ��OΪ����ԭ�㣩������������⣮
��ͼ���ڷ���ֽ�У�С�����εı߳�Ϊ1������ABC�����������Ϊ��㣬����ABC��x������ƽ��5����λ���ȣ�����������ֱ������ϵ��OΪ����ԭ�㣩������������⣮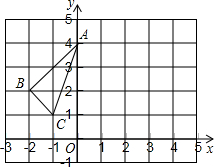 ��ͼ�ڱ߳�Ϊ1����λ���ȵ�С��������ɵ������У���������ABC�������������ߵĽ��㣩
��ͼ�ڱ߳�Ϊ1����λ���ȵ�С��������ɵ������У���������ABC�������������ߵĽ��㣩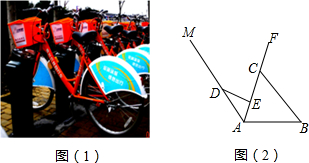
 ��ͼ��E��F�ֱ���AB��CD��һ�㣬��2=��D����1���C���࣬BC��AB����˵��AB��CD��
��ͼ��E��F�ֱ���AB��CD��һ�㣬��2=��D����1���C���࣬BC��AB����˵��AB��CD��