题目内容
11.某商店经销《超能陆战队》超萌“小白”玩具,“小白”玩具每个进价60元,每个玩具不得低于80元出售.销售“小白”玩具的单价m (元/个)与销售数量n (个)之间的函数关系如图所示.(1)试解释线段AB所表示的实际优惠销售政策;
(2)写出该店当一次销售n(n>10)个时,所获利润w(元)与n(个)之间的函数关系式;
(3)店长经过一段时间的销售发现:卖25个赚的钱反而比卖30个赚的钱多,你能用数学知识解释这一现象吗?为了不出现这种现象,在其他条件不变的情况下,店长应把最低价每个80元至少提高到多少元?
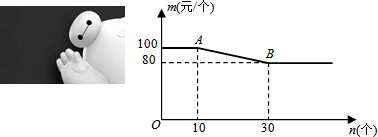
分析 (1)利用待定系数法求线段AB的函数的解析式,设m=kx+b,把A(10,100)和B(30,80)代入上式得到关于k、b的方程组,解方程组求出解析式;然后根据解析式解释线段AB所表示的实际优惠销售政策即可;
(2)分类讨论:当10<n<30时,W=(m-60)n;当n≥30时,W=(80-60)n;
(3)配方W=-n2+50n得到W=-(n-25)2+625,根据二次函数的性质讨论增减性,可得卖26个赚的钱反而比卖30个赚的钱多.为了不出现这种现象,在其他条件不变的情况下,店长应把最低价每个80元至少提高到85元.
解答 解:(1)设m=kx+b,
把A(10,100)和B(30,80)代入上式,得
$\left\{\begin{array}{l}{10k+b=100}\\{30k+b=80}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-1}\\{b=110}\end{array}\right.$,
∴线段AB的函数的解析式为m=-n+110(10≤n≤30);
由解析式可知线段AB所表示的实际优惠销售政策:一次性销售10到30个时,每多销售1个,玩具的单价下降1元;
(2)当10<n<30时,W=(m-60)n=(-n+110-60)n=-n2+50n,
当n≥30时,W=(80-60)n=20n;
(3)W=-n2+50n=-(n-25)2+625,
①当10<n≤25时,W随n的增大而增大,即卖的越多,利润越大;
②当25<n≤30时,W随n的增大而减小,即卖的越多,利润越小;
∴卖25个赚的钱反而比卖30个赚的钱多.
∴当n=25时,m=-n+110=85,
∴当每个玩具不得低于85元时,n的位置范围为10<n≤25,函数图象都在最对称轴左侧,W随n的增大而增大,即卖的越多,利润越大,
所以为了不出现这种现象,在其他条件不变的情况下,店长应把最低价每个80元至少提高到85元.
点评 本题考查了二次函数的应用:先得到二次函数的顶点式y=a(x-h)2+k,当a<0,x=h时,y有最大值k;当a<0,x=h时,y有最小值k;也考查了二次函数的增减性以及利用待定系数法求函数的解析式.熟练的运用二次函数的增减性质是解决问题的关键.

 如图,已知∠1=∠2,∠3=100°,则∠4=80°.
如图,已知∠1=∠2,∠3=100°,则∠4=80°. 如图,在正方形ABCD中,直角∠EAF的顶点与A重合,角的两边与CB的延长线、CD分别交于E、F两点,连接BF,直线BF与直线AE和对角线AC分别交于P、Q两点.若四边形AECF的面积为9,AF=$\sqrt{10}$,则PQ=$\frac{36\sqrt{13}}{35}$.
如图,在正方形ABCD中,直角∠EAF的顶点与A重合,角的两边与CB的延长线、CD分别交于E、F两点,连接BF,直线BF与直线AE和对角线AC分别交于P、Q两点.若四边形AECF的面积为9,AF=$\sqrt{10}$,则PQ=$\frac{36\sqrt{13}}{35}$.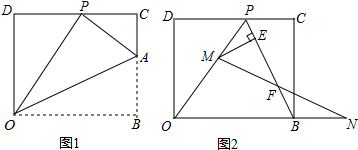

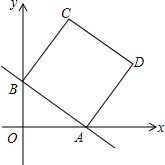 如图,在平面直角坐标系中,直线y=-$\frac{3}{4}$x+b分别与x轴、y轴交于点A、B,且点A的坐标为(8,0),四边形ABCD是正方形.
如图,在平面直角坐标系中,直线y=-$\frac{3}{4}$x+b分别与x轴、y轴交于点A、B,且点A的坐标为(8,0),四边形ABCD是正方形.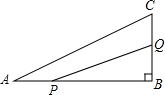 如图,在△ABC中,∠B=90°,AB=6cm,BC=3cm,点P以1cm/s的速度从点A开始沿边AB向点B移动,点Q以2cm/s的速度从点B开始沿边BC向点C移动,如果点P、Q分别从点A、B同时出发,多少时间后P、Q之间的距离等于4$\sqrt{2}$cm?
如图,在△ABC中,∠B=90°,AB=6cm,BC=3cm,点P以1cm/s的速度从点A开始沿边AB向点B移动,点Q以2cm/s的速度从点B开始沿边BC向点C移动,如果点P、Q分别从点A、B同时出发,多少时间后P、Q之间的距离等于4$\sqrt{2}$cm?