题目内容
3.若关于x、y的二元一次方程组$\left\{\begin{array}{l}2x+y=-3m+2\\ x+2y=-4\end{array}\right.$的解满足x-y>-3,求出满足条件的m的所有非负整数解.分析 将原方程组中两个方程相减可得x-y=-3m+6,由x-y>-3知-3m+6>-3,解该不等式求得m的范围,即可得满足条件的m的所有非负整数解.
解答 解:在关于x、y的二元一次方程组$\left\{\begin{array}{l}{2x+y=-3m+2}&{①}\\{x+2y=-4}&{②}\end{array}\right.$中,
①-②,得:x-y=-3m+6,
∵x-y>-3,
∴-3m+6>-3,
解得:m<3,
∴满足条件的m的所有非负整数解有0,1,2.
点评 本题主要考查解一元二次方程组和不等式的能力,根据题意得出关于m的不等式是解题的关键.

练习册系列答案
相关题目
13.下列说法正确的是( )
| A. | 方程3x=y-6的解是$\left\{\begin{array}{l}x=-2\\ y=0\end{array}\right.$ | B. | x=3是不等式组$\left\{\begin{array}{l}x-4≤0\\ 2x+3>0\end{array}\right.$的解 | ||
| C. | 如果$\frac{1}{3}$x<-1,那么x>-3 | D. | 不等式组$\left\{\begin{array}{l}x≤3\\ x≥3\end{array}\right.$无解 |
12.用1块A型钢板可制成2块C型钢板、1块D型钢板;用1块B型钢板可制成1块C型钢板、2块D型钢板.现需18块C型钢板,21块D型钢板,可恰好用A型钢板,B型钢板各多少块?设用A型钢板x块,B型钢板y块,可列方程组为( )
| A. | $\left\{\begin{array}{l}2x+y=18\\ x+2y=21\end{array}\right.$ | B. | $\left\{\begin{array}{l}x+y=18\\ 2x-y=21\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}2x+y=21\\ x+2y=18\end{array}\right.$ | D. | $\left\{\begin{array}{l}x+y=21\\ 2x+y=39\end{array}\right.$ |
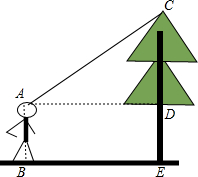 如图,在一次测量活动中,小丽站在离树底部E处5m的B处仰望树顶C,仰角为30°,已知小丽的眼睛离地面的距离AB为1.65m,那么这棵树大约有多高?(结果精确到0.1m,参考数据:$\sqrt{3}$≈1.73)
如图,在一次测量活动中,小丽站在离树底部E处5m的B处仰望树顶C,仰角为30°,已知小丽的眼睛离地面的距离AB为1.65m,那么这棵树大约有多高?(结果精确到0.1m,参考数据:$\sqrt{3}$≈1.73) 相等)
相等)