题目内容
19.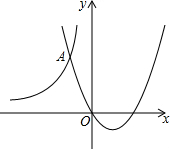 如图,抛物线y=(x-1)2-1与双曲线y=$\frac{k}{x}$交于点A(-1,m).
如图,抛物线y=(x-1)2-1与双曲线y=$\frac{k}{x}$交于点A(-1,m).(1)求k与m的值;
(2)写出点A关于抛物线y=(x-1)2-1的对称轴的对称点坐标(3,3).
分析 (1)根据自变量与函数值的关系,可得m的值,根据待定系数法,可得k的值;
(2)根据关于对称轴对称的两点的纵坐标相等,横坐标到对称轴的距离相等,可得答案.
解答 解:(1)当x=-1时,y=4-1=3,
即m=3.
A点的坐标为(-1,3),
将A点坐标代入双曲线,得
k=xy=-1×3=-3.
(2)点A关于抛物线y=(x-1)2-1的对称轴的对称点的横坐标为2-(-1)=3,纵坐标为3,
点A关于抛物线y=(x-1)2-1的对称轴的对称点的坐标(3,3).
故答案为:(3,3).
点评 本题考查了二次函数的性质,利用关于对称轴对称的两点的纵坐标相等,横坐标到对称轴的距离相等是解题关键.

练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
11.丽英是山区的孩子,她的家和学校在两座相邻的山顶上,去学校时先下坡再上坡,下坡路占全程的$\frac{1}{3}$,下坡速度是上坡速度的2倍,从家走到学校要花2个半小时,那么她从学校回家需要多少时间?( )
| A. | 2小时40分 | B. | 2个半小时 | C. | 2小时 | D. | 1小时40分 |
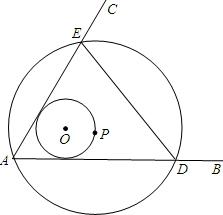 如图∠BAC=60°,半径长1的⊙0与∠BAC的两边相切,P为⊙O上一动点,以P为圆心,PA长为半径的⊙P交射线AB、AC于D、E两点,连接DE,则△EDA面积的最大值为$\frac{27\sqrt{3}}{4}$.
如图∠BAC=60°,半径长1的⊙0与∠BAC的两边相切,P为⊙O上一动点,以P为圆心,PA长为半径的⊙P交射线AB、AC于D、E两点,连接DE,则△EDA面积的最大值为$\frac{27\sqrt{3}}{4}$.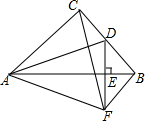 如图所示,在等腰Rt△ABC中,∠ACB=90°,D为BC的中点,DE⊥AB,垂足为点E,过点B作BF∥AC交DE的延长线于点F,连结CF、AD.
如图所示,在等腰Rt△ABC中,∠ACB=90°,D为BC的中点,DE⊥AB,垂足为点E,过点B作BF∥AC交DE的延长线于点F,连结CF、AD.