题目内容
6.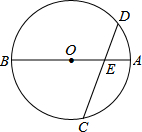 如图,AB为⊙O的直径,弦CD与AB相交于点E,且OE=DE,试确定$\widehat{BC}$与$\widehat{AD}$之间的数量关系.
如图,AB为⊙O的直径,弦CD与AB相交于点E,且OE=DE,试确定$\widehat{BC}$与$\widehat{AD}$之间的数量关系.
分析 连结OC、OD,如图,由OE=DE得到∠1=∠D,则利用三角形外角性质可得∠2=∠1+∠D=2∠1,再由OC=OD得到∠D=∠C,则∠C=∠1,然后利用三角形外角性质得∠BOC=3∠1,则根据圆心角、弧、弦的关系得到$\widehat{BC}$=3$\widehat{AD}$.
解答  解:连结OC、OD,如图,
解:连结OC、OD,如图,
∵OE=DE,
∴∠1=∠D,
∴∠2=∠1+∠D=2∠1,
∵OC=OD,
∴∠D=∠C,
∴∠C=∠1,
∵∠BOC=∠C+∠2,
∴∠BOC=3∠1,
∴$\widehat{BC}$=3$\widehat{AD}$.
点评 本题考查了圆心角、弧、弦的关系:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.

练习册系列答案
相关题目
16. 如图,双曲线y=$\frac{4}{x}$与正比例函数y=kx的图象交于A,B两点,过点A作AC⊥y轴于点C,连接BC,则△ABC的面积为( )
如图,双曲线y=$\frac{4}{x}$与正比例函数y=kx的图象交于A,B两点,过点A作AC⊥y轴于点C,连接BC,则△ABC的面积为( )
 如图,双曲线y=$\frac{4}{x}$与正比例函数y=kx的图象交于A,B两点,过点A作AC⊥y轴于点C,连接BC,则△ABC的面积为( )
如图,双曲线y=$\frac{4}{x}$与正比例函数y=kx的图象交于A,B两点,过点A作AC⊥y轴于点C,连接BC,则△ABC的面积为( )| A. | 2 | B. | $\frac{1}{2}$ | C. | 4 | D. | $\frac{1}{4}$ |
17.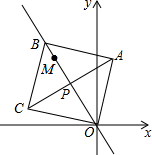 如图,点M(-3,4),点P从O点出发,沿射线OM方向1个单位/秒匀速运动,运动的过程中以P为对称中心,O为一个顶点作正方形OABC,当正方形面积为128时,点A坐标是( )
如图,点M(-3,4),点P从O点出发,沿射线OM方向1个单位/秒匀速运动,运动的过程中以P为对称中心,O为一个顶点作正方形OABC,当正方形面积为128时,点A坐标是( )
 如图,点M(-3,4),点P从O点出发,沿射线OM方向1个单位/秒匀速运动,运动的过程中以P为对称中心,O为一个顶点作正方形OABC,当正方形面积为128时,点A坐标是( )
如图,点M(-3,4),点P从O点出发,沿射线OM方向1个单位/秒匀速运动,运动的过程中以P为对称中心,O为一个顶点作正方形OABC,当正方形面积为128时,点A坐标是( )| A. | ($\frac{3}{2}$,$\frac{65}{6}$) | B. | ($\sqrt{7}$,11) | C. | (2,2$\sqrt{31}$) | D. | ($\frac{8}{5}$,$\frac{56}{5}$) |
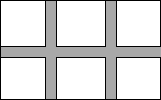 华泰新村开发商为促销商品房,决定在新村所在地的一块60m×100m的长方形空地上种植花草,且铺设三条如图所示的鹅卵石甬道,已知修建甬道后,剩下的草地面积为5568m2,求甬道的宽.
华泰新村开发商为促销商品房,决定在新村所在地的一块60m×100m的长方形空地上种植花草,且铺设三条如图所示的鹅卵石甬道,已知修建甬道后,剩下的草地面积为5568m2,求甬道的宽.