题目内容
16. 如图,双曲线y=$\frac{4}{x}$与正比例函数y=kx的图象交于A,B两点,过点A作AC⊥y轴于点C,连接BC,则△ABC的面积为( )
如图,双曲线y=$\frac{4}{x}$与正比例函数y=kx的图象交于A,B两点,过点A作AC⊥y轴于点C,连接BC,则△ABC的面积为( )| A. | 2 | B. | $\frac{1}{2}$ | C. | 4 | D. | $\frac{1}{4}$ |
分析 根据反比例函数的性质可判断点A与点B关于原点对称,则S△BOC=S△AOC,再利用反比例函数k的几何意义得到S△AOC=2,则易得S△ABC=4.
解答 解:∵双曲线y=$\frac{4}{x}$与正比例函数y=kx的图象交于A,B两点,
∴点A与点B关于原点对称,
∴S△BOC=S△AOC,
而S△AOC=$\frac{1}{2}$×4=2,
∴S△ABC=2S△AOC=4.
故选C.
点评 本题考查了反比例函数与一次函数的交点问题:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.

练习册系列答案
相关题目
5.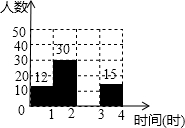 阅读对人的影响是巨大的,一本好书往往能改变一个人的一生.某校为了解全校1800名学生双休日的阅读时间,学校随机调查了七、八、九年级部分同学,并用得到的数据绘制成不完整的统计图表如图所示:
阅读对人的影响是巨大的,一本好书往往能改变一个人的一生.某校为了解全校1800名学生双休日的阅读时间,学校随机调查了七、八、九年级部分同学,并用得到的数据绘制成不完整的统计图表如图所示:
(1)x=40,y=0.18;
(2)请将频数分布直方图补充完整;
(3)根据调查数据估计,该校同学双休日阅读时间在2小时以上的学生的人数.
 阅读对人的影响是巨大的,一本好书往往能改变一个人的一生.某校为了解全校1800名学生双休日的阅读时间,学校随机调查了七、八、九年级部分同学,并用得到的数据绘制成不完整的统计图表如图所示:
阅读对人的影响是巨大的,一本好书往往能改变一个人的一生.某校为了解全校1800名学生双休日的阅读时间,学校随机调查了七、八、九年级部分同学,并用得到的数据绘制成不完整的统计图表如图所示:| 阅读时间 | 频数(人数) | 频率 |
| 0~1 | 12 | 0.12 |
| 1~2 | 30 | 0.3 |
| 2~3 | x | 0.4 |
| 3~4 | 18 | y |
| 合计 | m | 1 |
(2)请将频数分布直方图补充完整;
(3)根据调查数据估计,该校同学双休日阅读时间在2小时以上的学生的人数.




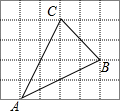 网格中的每个小正方形的边长都是1,△ABC每个顶点都在网格的交点处,
网格中的每个小正方形的边长都是1,△ABC每个顶点都在网格的交点处,
 如图,在Rt△ABC中,∠C=90°,∠A=30°,AC=2,则△ABC的面积=$\frac{2\sqrt{3}}{3}$.
如图,在Rt△ABC中,∠C=90°,∠A=30°,AC=2,则△ABC的面积=$\frac{2\sqrt{3}}{3}$.
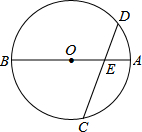 如图,AB为⊙O的直径,弦CD与AB相交于点E,且OE=DE,试确定$\widehat{BC}$与$\widehat{AD}$之间的数量关系.
如图,AB为⊙O的直径,弦CD与AB相交于点E,且OE=DE,试确定$\widehat{BC}$与$\widehat{AD}$之间的数量关系.